Đề kiểm tra giữa kì 1 Toán 9 - Đề số 8 có lời giải chi tiết — Không quảng cáo

Tải về đề thi và đáp án Tải về đề thi Tải về đáp án

Đề bài

Bài 1 (2 điểm) Thực hiện phép tính

a) $A = 3\sqrt {125} + \sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}}$

b) $B = \left( {2 + \sqrt 7 } \right)\sqrt {11 - 4\sqrt 7 } - \frac{{\sqrt {20} + 5}}{{\sqrt 5 + 2}}$

c) $C = {\sin ^2}{25^0} + {\sin ^2}{65^0} - \tan {35^0} + \cot {55^0} - \frac{{\cot {{32}^0}}}{{\tan {{58}^0}}}$

Bài 2 ( 1,5 điểm) Giải các phương trình sau:

a) $\sqrt {9x - 27} - \sqrt {x - 3} = 6$.

b) $\sqrt {{x^2} + 2x + 1} - \sqrt {x + 1} = 0$.

Bài 3 (2 ,5 điểm) Cho hai biểu thức $A = \frac{{\sqrt x - 2}}{{x + \sqrt x + 1}}$ và $B = \frac{{2\sqrt x }}{{\sqrt x - 2}} - \frac{{5\sqrt x - 2}}{{x - 2\sqrt x }} - \frac{{\sqrt x + 1}}{{\sqrt x }}$ với $x > 0;\,x \ne 4$

1) Tính giá trị biểu thức $A$ khi $x = 9$ .

2) Rút gọn biểu thức $B$ .

3) Tìm các giá trị của $x$ để $B \le - \frac{1}{2}$ .

4) Tìm giá trị lớn nhất của biểu thức $M = \frac{{6A}}{B}$ .

Bài 4 (3,5 điểm)

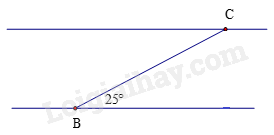
1) Một con thuyền đi qua một khúc sông theo hướng từ $B$ đến $C$ (như hình vẽ) với vận tốc $3,5km/h$ trong $12$ phút. Biết rằng đường đi của thuyền tạo với bờ sông một góc $25^\circ$ . Hãy tính chiều rộng của khúc sông ? (Kết quả tính theo đơn vị $km$ ,làm tròn kết quả đến chữ số thập phân thứ hai).

2) Cho tam giác $ABC$ nhọn có đường cao $AH$ . Gọi $E$ là hình chiếu của $H$ trên $AB$ .

a. Biết $AE = 3,6cm$ ; $BE = 6,4cm$ . Tính $AH,EH$ và góc $B.$ (Số đo góc làm tròn đến độ)

b. Kẻ $HF$ vuông góc với $AC$ tại $F.$ Chứng minh $AB.AE = AC.AF.$

c. Đường thẳng qua $A$ và vuông góc với $EF$ cắt $BC$ tại $D$ ; $EF$ cắt $AH$ tại $O.$ Chứng minh rằng ${S_{ADC}} = \frac{{{S_{AOE}}}}{{{{\sin }^2}B.{{\sin }^2}C}}$

Bài 5 (0,5 điểm) Giải phương trình $2\sqrt {2x - 1} = 8 - \sqrt[3]{{x + 3}}$ .

-------- Hết --------

Lời giải chi tiết

Bài 1 (2 điểm) Thực hiện phép tính

a) $A = 3\sqrt {125} + \sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}}$

b) $B = \left( {2 + \sqrt 7 } \right)\sqrt {11 - 4\sqrt 7 } - \frac{{\sqrt {20} + 5}}{{\sqrt 5 + 2}}$

c) $C = {\sin ^2}{25^0} + {\sin ^2}{65^0} - \tan {35^0} + \cot {55^0} - \frac{{\cot {{32}^0}}}{{\tan {{58}^0}}}$

Phương pháp

a) Đưa về trị tuyệt đối để tính toán.

b) Đưa nhân tử chung ra ngoài, rút gọn mẫu số và đưa về trị tuyệt đối để tính toán.

c) Biến đổi các tỉ số lượng giác về cùng số đo góc để tính toán.

Lời giải

a) $A = 3\sqrt {125} + \sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} = 15\sqrt 5 + \left| {2 - \sqrt 5 } \right| = 15\sqrt 5 + \sqrt 5 - 2 = 2\left( {8\sqrt 5 - 1} \right)$

b)

$\begin{array}{l}B = \left( {2 + \sqrt 7 } \right)\sqrt {11 - 4\sqrt 7 } - \frac{{\sqrt {20} + 5}}{{\sqrt 5 + 2}}\\\,\,\,\, = \left( {2 + \sqrt 7 } \right)\sqrt {{{\left( {2 - \sqrt 7 } \right)}^2}} - \frac{{2\sqrt 5 + {{\left( {\sqrt 5 } \right)}^2}}}{{\left( {\sqrt 5 + 2} \right)}}\\\,\,\,\, = \left( {2 + \sqrt 7 } \right)\left| {2 - \sqrt 7 } \right| - \frac{{\sqrt 5 \left( {2 + \sqrt 5 } \right)}}{{\left( {\sqrt 5 + 2} \right)}}\\\,\,\,\, = \left( {2 + \sqrt 7 } \right)\left( {\sqrt 7 - 2} \right) - \sqrt 5 \\\,\,\,\, = 7 - 4 - \sqrt 5 = 3 - \sqrt 5 \end{array}$

c) $C = {\sin ^2}{25^0} + {\sin ^2}{65^0} - \tan {35^0} + \cot {55^0} - \frac{{\cot {{32}^0}}}{{\tan {{58}^0}}}$

$C = {\sin ^2}{25^0} + co{s^2}{25^0} - \tan {35^0} + \tan {35^0} - \frac{{\cot {{32}^0}}}{{\cot {{32}^0}}} = 1 + 0 - 1 = 0$ .

Bài 2 ( 1,5 điểm) Giải các phương trình sau:

a) $\sqrt {9x - 27} - \sqrt {x - 3} = 6$.

b) $\sqrt {{x^2} + 2x + 1} - \sqrt {x + 1} = 0$.

Phương pháp

Xác định điều kiện xác định của phương trình.

a) Đưa các hệ số ra ngoài căn, nhóm nhân tử chung để tìm x.

b) Sử dụng hằng đẳng thức, nhóm nhân tử chung để tìm x.

Lời giải

a) $\sqrt {9x - 27} - \sqrt {x - 3} = 6$ (ĐKXĐ: $x \ge 3$ )

$\Leftrightarrow 3\sqrt {x - 3} - \sqrt {x - 3} = 6$

$\Leftrightarrow 2\sqrt {x - 3} = 6$

$\Leftrightarrow \sqrt {x - 3} = 3$

$\Leftrightarrow x - 3 = 9$

$\Leftrightarrow x = 12$ (thỏa mãn ĐKXĐ)

Vậy $x \in \left\{ {12} \right\}$ .

b) $\sqrt {{x^2} + 2x + 1} - \sqrt {x + 1} = 0$ ( ĐKXĐ: $x \ge - 1$ )

$\Leftrightarrow \sqrt {{{\left( {x + 1} \right)}^2}} - \sqrt {x + 1} = 0$

$\Leftrightarrow \sqrt {x + 1} \left( {\sqrt {x + 1} - 1} \right) = 0$

$\Leftrightarrow \left[ \begin{array}{l}\sqrt {x + 1} = 0\\\sqrt {x + 1} - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x + 1 = 0\\x + 1 = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\,\,\,(TM)\\x = 0\,\,\,\,(TM)\end{array} \right.$

Vậy $x \in \left\{ { - 1;0} \right\}$ .

Bài 3 (2 ,5 điểm) Cho hai biểu thức $A = \frac{{\sqrt x - 2}}{{x + \sqrt x + 1}}$ và $B = \frac{{2\sqrt x }}{{\sqrt x - 2}} - \frac{{5\sqrt x - 2}}{{x - 2\sqrt x }} - \frac{{\sqrt x + 1}}{{\sqrt x }}$ với $x > 0;\,x \ne 4$

1) Tính giá trị biểu thức $A$ khi $x = 9$ .

2) Rút gọn biểu thức $B$ .

3) Tìm các giá trị của $x$ để $B \le - \frac{1}{2}$ .

4) Tìm giá trị lớn nhất của biểu thức $M = \frac{{6A}}{B}$ .

Phương pháp

1) Kiểm tra x = 9 có thỏa mãn điều kiện hay không, sau đó thay vào biểu thức A để tính.

2) Xác định mẫu thức chung, quy đồng và thực hiện các phép toán với các phân thức đại số.

3) Thay biểu thức B vào $B \le - \frac{1}{2}$ .

$\frac{{f\left( x \right)}}{{g\left( x \right)}} \le 0$ $\Leftrightarrow f\left( x \right) \ge 0,g\left( x \right) < 0$ hoặc $f\left( x \right) \le 0,g\left( x \right) > 0$

4) Tính $M = \frac{{6A}}{B}$ . Chia cả tử và mẫu cho $\sqrt x$ rồi sử dụng bất đẳng thức Cosi: $a + \frac{1}{a} \ge 2$ .

Lời giải

1) Khi $x = 9 \Rightarrow \sqrt x = 3$ thỏa mãn điều kiện.

Thay vào biểu thức $A$ ta được:

$A = \frac{{3 - 2}}{{9 + 3 + 1}} = \frac{1}{{13}}$ .

Vậy khi $x = 9$ thì $A = \frac{1}{{13}}$ .

2) Với $x > 0;\,x \ne 4$ ta có: $B = \frac{{2\sqrt x }}{{\sqrt x - 2}} - \frac{{5\sqrt x - 2}}{{x - 2\sqrt x }} - \frac{{\sqrt x + 1}}{{\sqrt x }}$

$= \frac{{2\sqrt x }}{{\sqrt x - 2}} - \frac{{5\sqrt x - 2}}{{\sqrt x \left( {\sqrt x - 2} \right)}} - \frac{{\sqrt x + 1}}{{\sqrt x }}$

$= \frac{{2\sqrt x .\sqrt x }}{{\sqrt x \left( {\sqrt x - 2} \right)}} - \frac{{5\sqrt x - 2}}{{\sqrt x \left( {\sqrt x - 2} \right)}} - \frac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 2} \right)}}{{\sqrt x \left( {\sqrt x - 2} \right)}}$

$= \frac{{2x - \left( {5\sqrt x - 2} \right) - \left( {\sqrt x + 1} \right)\left( {\sqrt x - 2} \right)}}{{\sqrt x \left( {\sqrt x - 2} \right)}}$

$= \frac{{2x - 5\sqrt x + 2 - x + \sqrt x + 2}}{{\sqrt x \left( {\sqrt x - 2} \right)}}$

$= \frac{{x - 4\sqrt x + 4}}{{\sqrt x \left( {\sqrt x - 2} \right)}} = \frac{{{{\left( {\sqrt x - 2} \right)}^2}}}{{\sqrt x \left( {\sqrt x - 2} \right)}} = \frac{{\sqrt x - 2}}{{\sqrt x }}$

Vậy $B = \frac{{\sqrt x - 2}}{{\sqrt x }}$ với $x > 0;x \ne 4$

3) Với $x > 0;x \ne 4$ để $B \le - \frac{1}{2} \Leftrightarrow \frac{{\sqrt x - 2}}{{\sqrt x }} \le - \frac{1}{2} \Leftrightarrow \frac{{\sqrt x - 2}}{{\sqrt x }} + \frac{1}{2} \le 0 \Leftrightarrow \frac{{2\sqrt x - 4 + \sqrt x }}{{2\sqrt x }} \le 0$

$\Leftrightarrow \frac{{3\sqrt x - 4}}{{2\sqrt x }} \le 0$ mà $2\sqrt x > 0$ nên $3\sqrt x - 4 \le 0 \Leftrightarrow 3\sqrt x \le 4 \Leftrightarrow \sqrt x \le \frac{4}{3} \Leftrightarrow x \le \frac{{16}}{9}$

Kết hợp với điều kiện ta được $0 < x \le \frac{{16}}{9}$ thì $B \le - \frac{1}{2}$

4) Ta có: $M = \frac{{6A}}{B} = \frac{{6\left( {\sqrt x - 2} \right)}}{{x + \sqrt x + 1}}:\frac{{\sqrt x - 2}}{{\sqrt x }} = \frac{{6\left( {\sqrt x - 2} \right)}}{{x + \sqrt x + 1}}.\frac{{\sqrt x }}{{\sqrt x - 2}} = \frac{{6\sqrt x }}{{x + \sqrt x + 1}}$

$\Rightarrow M = \frac{6}{{\sqrt x + \frac{1}{{\sqrt x }} + 1}}$ do $x > 0 \Rightarrow \sqrt x > 0;\frac{1}{{\sqrt x }} > 0$ .

Áp dụng bất đẳng thức Cô si với 2 số dương ta được:

$\sqrt x + \frac{1}{{\sqrt x }} \ge 2\sqrt {\sqrt x .\frac{1}{{\sqrt x }}} = 2 \Rightarrow \sqrt x + \frac{1}{{\sqrt x }} + 1 \ge 3 \Leftrightarrow \frac{6}{{\sqrt x + \frac{1}{{\sqrt x }} + 1}} \le 2$ hay $M \le 2$

Dấu "=” xảy ra $\sqrt x = \frac{1}{{\sqrt x }} \Rightarrow x = 1$ ( thỏa mãn đk)

Vậy Max $M = 2 \Leftrightarrow x = 1$ .

Bài 4 (3,5 điểm)

1) Một con thuyền đi qua một khúc sông theo hướng từ $B$ đến $C$ (như hình vẽ) với vận tốc $3,5km/h$ trong $12$ phút. Biết rằng đường đi của thuyền tạo với bờ sông một góc $25^\circ$ . Hãy tính chiều rộng của khúc sông ? (Kết quả tính theo đơn vị $km$ ,làm tròn kết quả đến chữ số thập phân thứ hai).

2) Cho tam giác $ABC$ nhọn có đường cao $AH$ . Gọi $E$ là hình chiếu của $H$ trên $AB$ .

a. Biết $AE = 3,6cm$ ; $BE = 6,4cm$ . Tính $AH,EH$ và góc $B.$ (Số đo góc làm tròn đến độ)

b. Kẻ $HF$ vuông góc với $AC$ tại $F.$ Chứng minh $AB.AE = AC.AF.$

c. Đường thẳng qua $A$ và vuông góc với $EF$ cắt $BC$ tại $D$ ; $EF$ cắt $AH$ tại $O.$ Chứng minh rằng ${S_{ADC}} = \frac{{{S_{AOE}}}}{{{{\sin }^2}B.{{\sin }^2}C}}$

Phương pháp

1. Kẻ CH vuông góc với bờ sông tại H, ta có CH $\bot$ BH. CH chính là chiều rộng của khúc sông. Sử dụng định nghĩa tỉ số lượng giác của góc nhọn để suy ra chiều rộng của khúc sông.

2.

a. Sử dụng hệ thức lượng và tỉ số lượng giác để tính.

b. Sử dụng hệ thức lượng để chứng minh.

c. Chứng minh $\Delta A\text{EF} \backsim \Delta ACB\,\,(c.g.c)$ $\Rightarrow \Delta ADC \backsim \Delta AOE\,\,(g.g)$, ta có tỉ số diện tích của tam giác ADC và tam giác AOE => đpcm.

Lời giải

1)

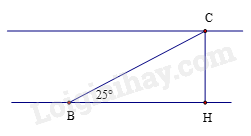
Đổi: 12 phút = $\frac{1}{5}$ giờ

Gọi chiều rộng của khúc sông là $CH$ . Đường đi của con thuyền là $BK$ suy ra $CH \bot BK\,\,,\,\,\widehat {CBH} = {25^0}$

Quãng đường BC dài là: $3,5\,.\,\frac{1}{5} = 0,7\,\,\left( {km} \right)$

Xét $\Delta BHC$ vuông tại H có: $CH = \sin {25^0}.\,\,BC = \,\sin {25^0}.\,0,7 \approx 0,29\,\,\left( {km} \right)$

Vậy chiều rộng khúc sông khoảng 0,29 (km).

2)

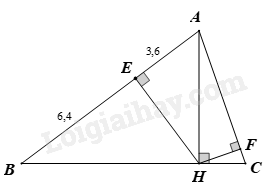
a. Ta có: $AB = AE + EB = 3,6 + 6,4 = 10cm$

Áp dụng hệ thức lượng trong tam giác vuông $AHB$ có $\widehat {AHB} = 90^\circ ;HE \bot AB$

Ta có: $A{H^2} = AE.AB$

$\Rightarrow AH = \sqrt {3,6.10} = \sqrt {36} = 6cm$

Và: $E{H^2} = AE.EB$

$\Rightarrow EH = \sqrt {3,6.6,4} = 4,8cm$

$\begin{array}{l}{\mathop{\rm Sin}\nolimits} B = \frac{{AH}}{{AB}} = \frac{6}{{10}} = 0,6\\ \Rightarrow \widehat B \approx 36^\circ 52'\end{array}$

b. Xét $\Delta ABH$ có : $\widehat {AHB} = 90^\circ ;HE \bot AB$

Áp dụng hệ thức lượng trong tam giác vuông ta có:

$AB.AE = A{H^2}$ (1)

Áp dụng hệ thức lượng trong tam giác vuông $AHC$ có: $\widehat {AHC} = 90^\circ ;HF \bot AC$

$\Rightarrow AF.AC = A{H^2}$ (2)

Từ (1) và (2) $\Rightarrow AB.AE = AC.AF$ (dpcm).

c)

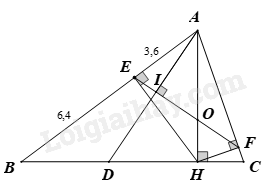
Gọi I là giao điểm của $AD$ và $EF$

Ta có: $AE.AB = {\rm{AF}}.AC \Rightarrow \frac{{AE}}{{AC}} = \frac{{{\rm{AF}}}}{{AB}}$

Dễ dàng chứng minh được $\Delta A\text{EF} \backsim \Delta ACB\,\,(c.g.c)$

$\Rightarrow \widehat {AFI} = \widehat {ABH;}\widehat {ACD} = \widehat {AEO}$ (1)

Mà $\widehat {CAD} + \widehat {{\rm{AF}}I} = {90^0}$

$\widehat {EAO} + \widehat {ABH} = {90^0}$

$\Rightarrow \widehat {EAO} = \widehat {CAD}$ (2)

Từ $(1);(2)\Rightarrow \Delta ADC \backsim \Delta AOE\,\,(g.g)$

$\Rightarrow \frac{{{S_{ADC}}}}{{{S_{AOE}}}} = {\left( {\frac{{AC}}{{AE}}} \right)^2} = {\left( {\frac{{AC}}{{AH}}.\frac{{AH}}{{AE}}} \right)^2} = \frac{{A{C^2}}}{{A{H^2}}}.\frac{{A{H^2}}}{{A{E^2}}}$

$\Rightarrow {S_{ADC}} = \frac{{{S_{AOE}}}}{{{{\left( {\frac{{AH}}{{AC}}} \right)}^2}.{{\left( {\frac{{AE}}{{AH}}} \right)}^2}}} = \frac{{{S_{AOE}}}}{{{{\sin }^2}C.c{\rm{o}}{{\rm{s}}^2}\widehat {EAO}}} = \frac{{{S_{AOE}}}}{{{{\sin }^2}C.{{\sin }^2}B}}$ (đpcm)

Bài 5 (0,5 điểm) Giải phương trình $2\sqrt {2x - 1} = 8 - \sqrt[3]{{x + 3}}$ .

Phương pháp

Tìm điều kiện xác định.

Đặt $\sqrt {2x - 1} = u \Rightarrow {u^2} = 2x - 1$ ; $\sqrt[3]{{x + 3}} = v \Rightarrow {v^3} = x + 3 \Leftrightarrow 2{v^3} = 2x + 6$ . Giải phương trình theo u và v.

Lời giải

Điều kiện $2x - 1 \ge 0 \Leftrightarrow x \ge \frac{1}{2}$ .

Đặt $\sqrt {2x - 1} = u \Rightarrow {u^2} = 2x - 1$ .

$\sqrt[3]{{x + 3}} = v \Rightarrow {v^3} = x + 3 \Leftrightarrow 2{v^3} = 2x + 6$ .

$\Rightarrow 2{v^3} - {u^2} = 2x + 6 - \left( {2x - 1} \right) = 7$

$\Leftrightarrow 2{v^3} - {u^2} - 7 = 0$

Mà $2\sqrt {2x - 1} = 8 - \sqrt[3]{{x + 3}} \Leftrightarrow 2u = 8 - v \Leftrightarrow u = \frac{{8 - v}}{2}$ .

$\Rightarrow 2{v^3} - {\left( {\frac{{8 - v}}{2}} \right)^2} - 7 = 0$

$\Leftrightarrow 2{v^3} - \frac{{64 - 16v + {v^2}}}{4} - 7 = 0$

$\Leftrightarrow 8{v^3} - 64 + 16v - {v^2} - 28 = 0$

$\Leftrightarrow 8{v^3} - {v^2} + 16v - 92 = 0$

$\Leftrightarrow \left( {v - 2} \right)\left( {8{v^2} + 15v + 46} \right) = 0$

$\Leftrightarrow v = 2$

$\Leftrightarrow x + 3 = 8$

$\Leftrightarrow x = 5$ (thỏa mãn điều kiện).

Vậy $x = 5$ .