Đề thi giữa kì 1 Toán 9 - Đề số 2 — Không quảng cáo

Cặp số \(\left( {{x_0};{y_0}} \right)\) là nghiệm của phương trình bậc nhất hai ẩn \(ax + by = c\) nếu \(a{x_0} + b{y_0} = c\).

Ta có: \(\left( { - 2} \right) + 2.1 = 0\) nên cặp số \(\left( {x;y} \right) = \left( { - 2;1} \right)\) là nghiệm của phương trình \(x + 2y = 0\).

Đáp án A.

Hệ phương trình \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) là hệ hai phương trình bậc nhất hai ẩn với \(ax + by = c\) và \(a'x + b'y = c'\) là hai phương trình bậc nhất hai ẩn.

Hệ phương trình \(\left\{ \begin{array}{l}{x^2} + {y^2} = 121\\x + 2y =  - 11\end{array} \right.\) không phải là hệ phương trình bậc nhất hai ẩn vì phương trình \({x^2} + {y^2} = 121\) không phải là phương trình bậc nhất hai ẩn.

Đáp án D.

Phương trình chứa ẩn ở mẫu có điều kiện là các mẫu thức khác 0.

Điều kiện xác định của phương trình \(\frac{6}{{{x^2} - 9}} + \frac{2}{{x - 3}} = 0\) là:

\({x^2} - 9 \ne 0\) và \(x - 3 \ne 0\)

hay \(x \ne  - 3\) và \(x \ne 3\).

Đáp án B.

Sử dụng phương pháp giải phương trình tích.

Để giải phương trình \(\left( {2x + 1} \right)\left( {x - 2} \right) = 0\), ta giải hai phương trình \(2x + 1 = 0\) và \(x - 2 = 0\)

+) \(2x + 1 = 0\) hay \(2x =  - 1\) suy ra \(x =  - \frac{1}{2}\);

+) \(x - 2 = 0\) suy ra \(x = 2\).

Vậy phương trình có nghiệm là \(x =  - \frac{1}{2};x = 2\).

Đáp án B.

Ta gọi hệ thức dạng \(a > b\) (hay \(a < b\), \(a \ge b\), \(a \le b\)) là bất đẳng thức và gọi a là vế trái, b là vế phải của bất đẳng thức.

Hệ thức \({y^2} \ge 0\) là bất đẳng thức.

Đáp án C.

- Khi nhân cả hai vế của một bất đẳng thức với cùng một số dương ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.

- Khi nhân cả hai vế của một bất đẳng thức với cùng một số âm ta được bất đẳng thức mới ngược chiều với bất đẳng thức đã cho.

Nếu \(c > 0\) thì \(ac \ge bc\) nên A sai, D đúng.

Nếu \(c < 0\) thì \(ac \le bc\) nên B và C sai.

Đáp án D.

Bất phương trình \(A\left( x \right) \ge B\left( x \right)\) có \(A\left( x \right)\) là vế trái, \(B\left( x \right)\) là vế phải.

\(6 - 11x\) là vế phải của bất phương trình.

Đáp án D.

Dựa vào cách giải bất phương trình.

Ta có:

\( - 2x + 6 > 0\)

\( - 2x >  - 6\)

\(x < 3\)

Vậy \(x = 2\) thỏa mãn bất phương trình \( - 2x + 6 > 0\).

Đáp án A.

Dựa vào kiến thức về tỉ số lượng giác trong tam giác vuông.

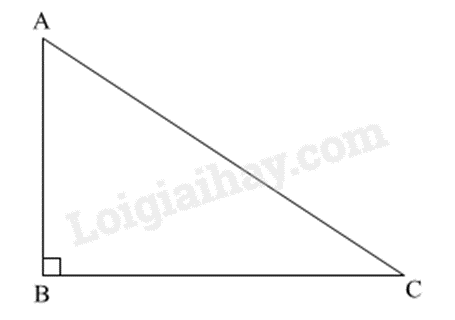
Áp dụng tỉ số lượng giác của tam giác vuông vào tam giác ABC, ta có: \(\sin C = \frac{{AB}}{{AC}}\).

Đáp án D.

Sử dụng định lí Pythagore để tính cạnh AC.

Sử dụng kiến thức về tỉ số lượng giác để tính cotB.

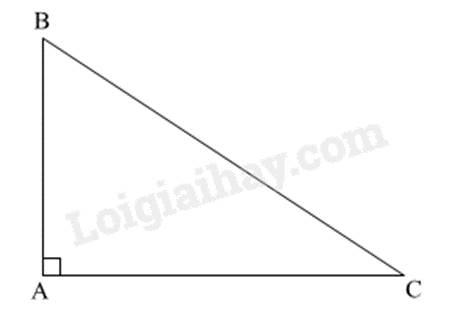
Áp dụng định lí Pythagore trong tam giác, ta có:

\(AC = \sqrt {B{C^2} - A{B^2}}  = \sqrt {{5^2} - {3^2}}  = \sqrt {16}  = 4\)

Tam giác ABC vuông tại A nên \(\cot B = \frac{{AB}}{{AC}} = \frac{3}{4}\).

Đáp án B.

Biểu diễn tỉ số lượng giác của góc ACB theo AC và BC. Từ đó ta tính được góc ACB.

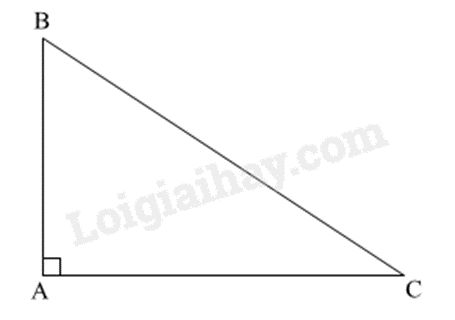
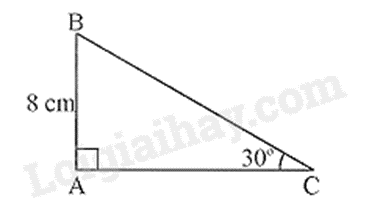
Trong tam giác ABC vuông tại A, ta có: \(\cos ACB = \frac{{AC}}{{BC}} = \frac{6}{{12}} = \frac{1}{2}\) suy ra \(\widehat {ACB} = 60^\circ \).

Đáp án D.

Biểu diễn cạnh BC theo AB và tỉ số lượng giác của góc C.

Độ dài cạnh BC là: \(BC = \frac{{AB}}{{\sin C}} = \frac{8}{{\sin 30^\circ }} = 16\left( {cm} \right)\).

Đáp án D.

1.

a) Đưa phương trình về phương trình tích để giải.

b) Quy đồng mẫu thức để giải phương trình.

c, d) Chuyển vế, sử dụng tính chất của bất đẳng thức để giải bất phương trình.

2. Sử dụng phương pháp cộng đại số để giải hệ phương trình.

1.

a) \({x^2} - 5x + 4\left( {x - 5} \right) = 0\)

\(\begin{array}{l}x\left( {x - 5} \right) + 4\left( {x - 5} \right) = 0\\\left( {x + 4} \right)\left( {x - 5} \right) = 0\end{array}\)

+) \(x + 4 = 0\) suy ra \(x =  - 4\)

+) \(x - 5 = 0\) suy ra \(x = 5\)

Vậy phương trình có nghiệm là \(x =  - 4;x = 5\).

b) \(\frac{x}{{x - 3}} = \frac{x}{{x + 3}} + \frac{{36}}{{{x^2} - 9}}\)

ĐKXĐ: \(x - 3 \ne 0\); \(x + 3 \ne 0\); \({x^2} - 9 \ne 0\) hay \(x \ne 3\) và \(x \ne  - 3\)

Ta có:\(\frac{x}{{x - 3}} = \frac{x}{{x + 3}} + \frac{{36}}{{{x^2} - 9}}\)

\(\begin{array}{l}\frac{{x\left( {x + 3} \right)}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} = \frac{{x\left( {x - 3} \right)}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} + \frac{{36}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\\x\left( {x + 3} \right) = x\left( {x - 3} \right) + 36\\{x^2} + 3x = {x^2} - 3x + 36\\{x^2} - {x^2} + 3x + 3x = 36\\6x = 36\\x = 6\end{array}\)

Vậy nghiệm của phương trình là \(x = 6\).

c) \(3x - 2 > 4\)

\(\begin{array}{l}3x > 4 + 2\\3x > 6\\x > 2\end{array}\)

Vậy nghiệm của bất phương trình là \(x > 2\).

d) \(\frac{{3x - 1}}{4} + 5 \le \frac{{x - 1}}{2}\)

\(\begin{array}{l}\frac{{3x - 1}}{4} + \frac{{20}}{4} \le \frac{{2\left( {x - 1} \right)}}{4}\\3x - 1 + 20 \le 2\left( {x - 1} \right)\\3x + 19 \le 2x - 2\\3x - 2x \le  - 2 - 19\\x \le  - 21\end{array}\)

Vậy nghiệm của bất phương trình là \(x \le  - 21\).

2. Giải hệ phương trình \(\left\{ \begin{array}{l}2x + y = 8\\x - y =  - 5\end{array} \right.\)

\(\begin{array}{l}\left\{ \begin{array}{l}2x + y = 8\\x - y =  - 5\end{array} \right.\\\left\{ \begin{array}{l}\left( {2x + x} \right) + \left( {y - y} \right) = 8 + \left( { - 5} \right)\\x - y =  - 5\end{array} \right.\\\left\{ \begin{array}{l}3x = 3\\x - y =  - 5\end{array} \right.\\\left\{ \begin{array}{l}x = 1\\1 - y =  - 5\end{array} \right.\\\left\{ \begin{array}{l}x = 1\\y = 6\end{array} \right.\end{array}\)

Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {1;6} \right)\)

Gọi số tiền bác An đầu tư cho khoản thứ nhất là \(x\) (triệu đồng),

số tiền bác An đầu tư cho khoản thứ hai là \(y\) (triệu đồng), \(\left( {x,y > 0} \right)\).

Biểu diễn hệ phương trình theo x và y.

Từ đó giải hệ phương trình.

Gọi số tiền bác An đầu tư cho khoản thứ nhất là \(x\) (triệu đồng),

số tiền bác An đầu tư cho khoản thứ hai là \(y\) (triệu đồng), \(\left( {x,y > 0} \right)\).

Vì bác An chia số tiền 600 triệu đồng của mình cho hai khoản đầu tư nên ta có phương trình:

\(x + y = 600\). (1)

Vì lãi suất cho khoản đầu tư thứ nhất là 6%/năm và khoản đầu tư thứ hai là 8%/năm và sau một năm, tổng tiền lãi thu được là 40 triệu đồng nên ta có phương trình:

\(6\% x + 8\% y = 40\) hay \(0,06x + 0,08y = 40\). (2)

Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 600\\0,06x + 0,08y = 40\end{array} \right.\).

Từ phương trình (1), ta có: \(y = 600 - x\).

Thế vào phương trình (2), ta được phương trình mới: \(0,06x + 0,08\left( {600 - x} \right) = 40\)

Suy ra \(0,06x + 0,08\left( {600 - x} \right) = 40\)

\(\begin{array}{l}0,06x + 48 - 0,08x = 40\\ - 0,02x = 40 - 48\\ - 0,02x =  - 8\\x = 400\end{array}\)

Suy ra \(y = 600 - 400 = 200\).

Vậy bác An đầu tư vào khoản thứ nhất 400 triệu đồng, khoản thứ hai 200 triệu đồng.

Kẻ đoạn thẳng DC biểu diễn cột cờ, các cọc và cột cờ cùng vuông góc với mặt đất.

Kéo dài đoạn thẳng AB, cắt DC tại H.

Chứng minh AB = MN = 10m.

Biểu diễn \(\cot DAH\) và \(\cot DBH\) theo tỉ số lượng giác của tam giác vuông \(DAH\) và \(DBH\).

Từ đó tính chiều cao cột cờ DC theo DH và HC.

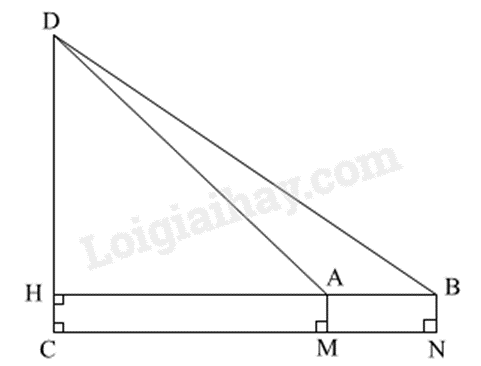
Kẻ DC là đoạn thẳng biểu diễn cột cờ, khi đó các cọc và cột cờ cùng vuông góc với mặt đất nên DC // AM // BN.

Xét tứ giác ABMN có AM // BN và  AM = BN = 1 m  nên ABMN là hình bình hành, suy ra \(AB = MN = 10m\), AB // MN.

Kéo dài AB cắt DC tại H, mà AB // MN nên AH // CN.

Mà \(DC \bot CN\) nên \(DH \bot HB\) hay \(\widehat {DHB} = 90^\circ \).

Xét tam giác DHA vuông tại H, ta có: \(\cot DAH = \frac{{AH}}{{DH}}\) suy ra \(AH = DH.\cot DAH\).

Xét tam giác DHB vuông tại H, ta có: \(\cot DBH = \frac{{BH}}{{DH}}\) suy ra \(BH = DH.\cot DBH\).

Ta có: \(AB = BH - AH\)

\(AB = DH.\cot DBH - DH.\cot DAH\)

\(AB = DH\left( {\cot DBH - \cot DAH} \right)\)

\(10 = DH\left( {\cot 43^\circ 16' - \cot 50^\circ 19'12''} \right)\)

\(DH = \frac{{10}}{{\cot 43^\circ 16' - \cot 50^\circ 19'12''}} \approx 42,96\left( m \right)\)

Tứ giác AMCH có \(\widehat M = \widehat C = \widehat H = 90^\circ \) nên tứ giác AMCH là hình chữ nhật, suy ra \(CH = AM = 1m\).

Vậy độ cao cột cờ DC là \(DC = DH + HC = 42,96 + 1 = 43,96\left( m \right)\).

a) Sử dụng kiến thức về tỉ số lượng giác và hệ thức lượng của tam giác vuông để giải.

b) Chứng minh \(BE.AB = A{H^2} = B{C^2} - C{H^2}\)

c) Chứng minh \(\widehat {ABH} = \widehat C\).

Biểu diễn tỉ số lượng giác \(\tan ABH\) theo HE và BE.

Từ đó chứng minh \(BF = BE.\tan C\).

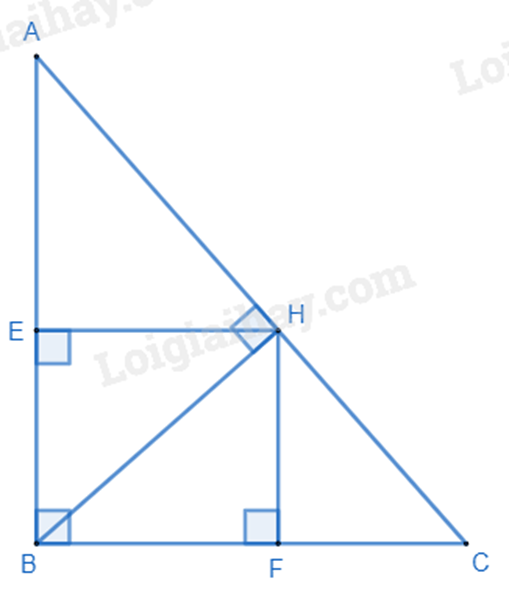
a) Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:

\(BC = \sqrt {A{C^2} - A{B^2}}  = \sqrt {{8^2} - {6^2}}  = 2\sqrt 7 \) (cm)

Áp dụng tỉ số lượng giác trong tam giác vuông ABC, ta có:

\(\sin ACB = \frac{{AB}}{{AC}} = \frac{6}{8} = \frac{3}{4}\)

Suy ra \(\widehat {ACB} \approx 49^\circ \)

Xét tam giác ABH vuông tại H, ta có:

\(\sin ACB = \frac{{BH}}{{BC}}\) suy ra \(\frac{{BH}}{{BC}} = \frac{3}{4}\)

Do đó \(BH = \frac{3}{4}BC = \frac{3}{4}.2\sqrt 7  = \frac{{6\sqrt 7 }}{4}\) (cm)

b) Xét tam giác BEH và tam giác BHA có:

\(\widehat {BEH} = \widehat {AHB}\left( { = 90^\circ } \right)\)

\(\widehat B\) chung

Suy ra $\Delta BEH\backsim \Delta BHA$ (g.g)

Suy ra \(\frac{{BE}}{{BH}} = \frac{{BH}}{{AB}}\), do đó \(BE.AB = B{H^2}\) (1)

Áp dụng định lí Pythagore vào tam giác BHC vuông tại H, ta có:

\(B{C^2} - H{C^2} = B{H^2}\) (2)

Từ (1) và (2) suy ra \(BE.BA = B{C^2} - H{C^2}\) (đpcm)

c) Ta có \(\widehat {ABH} = \widehat C\) (cùng phụ với \(\widehat A\))

Xét tứ giác BEHF có \(\widehat B = \widehat E = \widehat H = 90^\circ \) nên tứ giác BEHF là hình chữ nhật, suy ra \(HE = BF\).

Xét tam giác BHE, ta có: \(\tan HBE = \frac{{EH}}{{EB}}\) suy ra \(EH = BE.\tan HBE\)

Mà \(\widehat {HBE} = \widehat C\) và \(HE = BF\) (cmt) nên \(BF = BE.\tan C\) (đpcm).

Chứng minh \(\left( {1 - a} \right)\left( {1 - b} \right) > 1 - a - b\).

Tiếp tục chứng minh \(\left( {1 - a} \right)\left( {1 - b} \right)\left( {1 - c} \right) > 1 - a - b - c\).

Cuối cùng chứng minh \(\left( {1 - a} \right)\left( {1 - b} \right)\left( {1 - c} \right)\left( {1 - d} \right) > 1 - a - b - c - d\).

Ta có: \(\left( {1 - a} \right)\left( {1 - b} \right) = 1 - a - b + ab\).

Vì \(0 < a,b\) nên \(1 - a - b + ab > 1 - a - b\).

Vì \(c < 1\) nên \(1 - c > 0\), suy ra \(\left( {1 - a} \right)\left( {1 - b} \right)\left( {1 - c} \right) > \left( {1 - a - b} \right)\left( {1 - c} \right)\).

Ta có: \(\left( {1 - a - b} \right)\left( {1 - c} \right) = 1 - a - b - c + ac + bc\).

Vì \(0 < a,b,c\) nên \(1 - a - b - c + ac + bc > 1 - a - b - c\).

Lại có \(d < 1\) nên \(1 - d > 0\), suy ra \(\left( {1 - a} \right)\left( {1 - b} \right)\left( {1 - c} \right)\left( {1 - d} \right) > \left( {1 - a - b - c} \right)\left( {1 - d} \right)\)

Ta có: \(\left( {1 - a - b - c} \right)\left( {1 - d} \right) = 1 - a - b - c - d + ad + bd + cd\).

Vì \(0 < a,b,c,d\) nên \(1 - a - b - c - d + ad + bd + cd > 1 - a - b - c - d\).

Khi đó \(\left( {1 - a} \right)\left( {1 - b} \right)\left( {1 - c} \right)\left( {1 - d} \right) > 1 - a - b - c - d\).