Đề thi giữa kì 2 Toán 8 - Đề số 2 - Kết nối tri thức
Phần trắc nghiệm (2 điểm) Câu 1: Biểu thức nào sau đây không phải là phân thức đại số?
Đề bài
Biểu thức nào sau đây không phải là phân thức đại số?
-
A.
\(\frac{{5x - 6}}{{3x}}\) (với \(x \ne 0\)).
-
B.
\(\frac{{\frac{1}{{2x}}}}{{x + 1}}\) (với \(x \ne 0;x \ne - 1\)).
-
C.
\(\frac{{2x - 3y}}{{xyz}}\) (với \(xyz \ne 0\)).
-
D.
\(6{x^2} - 5x + 7\).
Điều kiện xác định của phân thức \(\frac{{3x - 5}}{{2x + 1}}\) là:
-
A.
\(x \ne \frac{{ - 1}}{2}\).
-
B.
\(x \ne \frac{1}{2}\).
-
C.
\(x \ne 0\).
-
D.
\(x \ne \frac{5}{3}\).
Tính giá trị của phân thức \(A\left( x \right) = \frac{3}{{x - 1}}\) với \(x \ne 1\) tại x = 2
-
A.
\(\frac{1}{3}\).
-
B.
\( - 3\).
-
C.
\(\frac{{ - 1}}{3}\).
-
D.
\(3\).
Thực hiện phép tính sau: \(\frac{{2x - 3}}{7} + \frac{{5x + 3}}{7}\), ta được kết quả là:
-
A.
\(x\).
-
B.
\(\frac{{ - 3x}}{7}\).
-
C.
\(\frac{x}{7}\).
-
D.
\(\frac{{3x}}{7}\).
Kết quả phép tính \(\frac{{8x}}{{15{y^3}}}:\left( { - \frac{{4{x^2}}}{{3{y^2}}}} \right)\) là
-
A.
\(\frac{{ - 1}}{{10xy}}\).
-
B.
\(\frac{{ - 2}}{{5x{y^2}}}\).
-
C.
\(\frac{{ - 2}}{{5xy}}\).
-
D.
\(\frac{2}{{5xy}}\).
-
A.
\({80^0}\).
-
B.
\({60^0}\).
-
C.
\({50^0}\).
-
D.
\({40^0}\).
Đâu là độ dài 3 cạnh của một tam giác vuông:
-
A.
4cm, 7cm, 6cm.
-
B.
6cm, 10cm, 8cm.
-
C.
20cm, 12cm, 25cm.
-
D.
6cm, 11cm, 9cm.
Một người cao 1,5 mét có bóng trên mặt đất dài 2,1 mét. Cùng lúc ấy, một cái cây gần đó có bóng trên mặt đất dài 4,2 mét. Tính chiều cao của cây.
-
A.
\(AB = 3m\).
-
B.
\(AB = 0,75m\).
-
C.
\(AB = 2,4m\).
-
D.
\(AB = 2,25m\).
Lời giải và đáp án
Biểu thức nào sau đây không phải là phân thức đại số?
-
A.
\(\frac{{5x - 6}}{{3x}}\) (với \(x \ne 0\)).
-
B.
\(\frac{{\frac{1}{{2x}}}}{{x + 1}}\) (với \(x \ne 0;x \ne - 1\)).
-
C.
\(\frac{{2x - 3y}}{{xyz}}\) (với \(xyz \ne 0\)).
-
D.
\(6{x^2} - 5x + 7\).
Đáp án : B
Phân thức đại số là biểu thức có dạng \(\frac{A}{B}\), trong đó A, B là những đa thức và B khác đa thức 0.
Ta có:
\(\frac{{5x - 6}}{{3x}}\) (với \(x \ne 0\)) là phân thức đại số vì 5x – 6; 3x là đa thức, 3x khác 0.
\(\frac{{\frac{1}{{2x}}}}{{x + 1}}\) (với \(x \ne 0;x \ne - 1\)) không phải phân thức đại số vì \(\frac{1}{{2x}}\) không phải là đa thức.
\(\frac{{2x - 3y}}{{xyz}}\) (với \(xyz \ne 0\)) là phân thức đại số vì 2x – 3y, xyz là đa thức và xyz khác 0.
\(6{x^2} - 5x + 7 = \frac{{6{x^2} - 5x + 7}}{1}\) là phân thức đại số.
Điều kiện xác định của phân thức \(\frac{{3x - 5}}{{2x + 1}}\) là:
-
A.
\(x \ne \frac{{ - 1}}{2}\).
-
B.
\(x \ne \frac{1}{2}\).
-
C.
\(x \ne 0\).
-
D.
\(x \ne \frac{5}{3}\).
Đáp án : A
Để phân thức xác định thì mẫu thức khác 0.
Phân thức \(\frac{{3x - 5}}{{2x + 1}}\) xác định khi \(2x + 1 \ne 0\) hay \(x \ne \frac{{ - 1}}{2}\).
Tính giá trị của phân thức \(A\left( x \right) = \frac{3}{{x - 1}}\) với \(x \ne 1\) tại x = 2
-
A.
\(\frac{1}{3}\).
-
B.
\( - 3\).
-
C.
\(\frac{{ - 1}}{3}\).
-
D.
\(3\).
Đáp án : D
Kiểm tra giá trị của x.
Thay giá trị của x vào phân thức để tính giá trị của A.
Ta có: \(x = 2 \ne 1\) thỏa mãn điều kiện xác định của A.
Thay x = 2 vào A, ta được:
\(A\left( 2 \right) = \frac{3}{{2 - 1}} = 3\).
Thực hiện phép tính sau: \(\frac{{2x - 3}}{7} + \frac{{5x + 3}}{7}\), ta được kết quả là:
-
A.
\(x\).
-
B.
\(\frac{{ - 3x}}{7}\).
-
C.
\(\frac{x}{7}\).
-
D.
\(\frac{{3x}}{7}\).
Đáp án : A
Để cộng hai phân thức cùng mẫu, ta cộng tử thức với nhau và giữ nguyên mẫu thức.
Ta có: \(\frac{{2x - 3}}{7} + \frac{{5x + 3}}{7} = \frac{{2x - 3 + 5x + 3}}{7} = \frac{{7x}}{7} = x\)
Kết quả phép tính \(\frac{{8x}}{{15{y^3}}}:\left( { - \frac{{4{x^2}}}{{3{y^2}}}} \right)\) là
-
A.
\(\frac{{ - 1}}{{10xy}}\).
-
B.
\(\frac{{ - 2}}{{5x{y^2}}}\).
-
C.
\(\frac{{ - 2}}{{5xy}}\).
-
D.
\(\frac{2}{{5xy}}\).
Đáp án : C
Sử dụng quy tắc chia hai phân thức.
Ta có: \(\frac{{8x}}{{15{y^3}}}:\left( { - \frac{{4{x^2}}}{{3{y^2}}}} \right)\)\( = \frac{{8x}}{{15{y^3}}}.\frac{{ - 3{y^2}}}{{4{x^2}}}\)\( = \frac{{2.4.\left( { - 3} \right)x{y^2}}}{{3.5.4{x^2}{y^3}}}\)\( = \frac{{ - 2}}{{5xy}}\).
-
A.
\({80^0}\).
-
B.
\({60^0}\).
-
C.
\({50^0}\).
-
D.
\({40^0}\).
Đáp án : D
Dựa vào định lí hai tam giác đồng dạng.
Định lí tổng ba góc trong một tam giác bằng \({180^0}\).
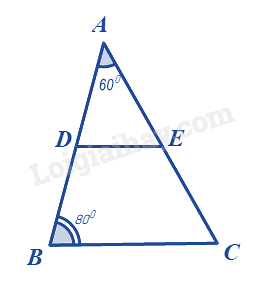
Ta có: DE // BC nên $\Delta ADE\backsim \Delta ABC$ (định lí hai tam giác đồng dạng)
\( \Rightarrow \widehat D = \widehat B = {80^0}\), \(\widehat E = \widehat C\)\( = {180^0} - \widehat A - \widehat B\)\( = {180^0} - {60^0} - {80^0}\)\( = {40^0}\)
Đâu là độ dài 3 cạnh của một tam giác vuông:
-
A.
4cm, 7cm, 6cm.
-
B.
6cm, 10cm, 8cm.
-
C.
20cm, 12cm, 25cm.
-
D.
6cm, 11cm, 9cm.
Đáp án : B
Áp dụng định lí Pythagore đảo trong tam giác.
Ta có:
\({4^2} + {6^2} = 52 \ne 49 = {7^2}\) nên tam giác này không phải là tam giác vuông.
\({6^2} + {8^2} = 100 = {10^2}\) nên tam giác này là tam giác vuông.
\({12^2} + {20^2} = 544 \ne 624 = {25^2}\) nên tam giác này không phải là tam giác vuông.
\({6^2} + {9^2} = 117 \ne 121 = {11^2}\) nên tam giác này không phải là tam giác vuông.
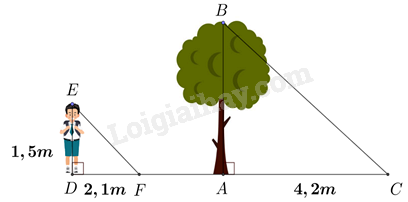
Một người cao 1,5 mét có bóng trên mặt đất dài 2,1 mét. Cùng lúc ấy, một cái cây gần đó có bóng trên mặt đất dài 4,2 mét. Tính chiều cao của cây.

-
A.
\(AB = 3m\).
-
B.
\(AB = 0,75m\).
-
C.
\(AB = 2,4m\).
-
D.
\(AB = 2,25m\).
Đáp án : A
Sử dụng các trường hợp đồng dạng của tam giác vuông.
Vì cùng thời điểm nên ta có \(\widehat F = \widehat C\).
Xét \(\Delta DEF\) và \(\Delta ABC\) có:
\(\widehat D = \widehat A\left( { = {{90}^0}} \right)\)
\(\widehat F = \widehat C\)
$\Rightarrow \Delta DEF\backsim \Delta ABC\left( g.g \right)$
\( \Rightarrow \frac{{DE}}{{AB}} = \frac{{DF}}{{AC}}\)
\(\frac{{1,5}}{{2,1}} = \frac{{AB}}{{4,2}} \Rightarrow AB = 4,2.\frac{{1,5}}{{2,1}} = 3\left( m \right)\).
a) Sử dụng các phép tính với phân thức để rút gọn A.
b) Kiểm tra điều kiện của x. Thay x = 2 vào A để tính A.
c) Để A nhận giá trị nguyên thì tử thức chia hết cho mẫu thức. Từ đó tìm giá trị của x.
a) Với \(x \ne \pm 1\), ta có:
\(\begin{array}{l}A = \left( {\frac{1}{{x - 1}} - \frac{1}{{x + 1}}} \right).\frac{{3x - 3}}{2}\\ = \frac{{\left( {x + 1} \right) - \left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}.\frac{{3\left( {x - 1} \right)}}{2}\\ = \frac{{x + 1 - x + 1}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}.\frac{{3\left( {x - 1} \right)}}{2}\\ = \frac{2}{{\left( {x - 1} \right)\left( {x + 1} \right)}}.\frac{{3\left( {x - 1} \right)}}{2}\\ = \frac{3}{{x + 1}}\end{array}\)
b) Ta có: \(x = 2\) (tmđk) nên thay \(x = 2\) vào biểu thức A, ta được:
\(A = \frac{3}{{2 + 1}} = \frac{3}{3} = 1\).
Vậy A = 1 khi x = 2.
c) Để A nhận giá trị nguyên thì \(3 \vdots \left( {x + 1} \right)\) hay \(x + 1 \in U\left( 3 \right)\). \(U\left( 3 \right) = \left\{ { \pm 1; \pm 3} \right\}\). Ta có bảng giá trị sau:

Vậy \(x \in \left\{ { - 4; - 2;0;2} \right\}\) thì biểu thức A nhận giá trị nguyên.
a,b Thời gian ca nô đi = quãng đường : vận tốc.
Vận tốc xuôi dòng = vận tốc thực + vận tốc dòng nước.
Vận tốc ngược dòng = vận tốc thực – vận tốc dòng nước.
c) Thời gian ca nô đi từ bến A đến bến B và từ bến B đến vị trí C = tổng thời gian đi hai đoạn đó.
Kiểm tra điều kiện của x, thỏa mãn thì thay vận tốc bằng 12 vào phân thức.
a) Vì vận tốc của ca nô là x nên vận tốc xuôi dòng của ca nô là x + 3 (km/h)
Vận tốc ngược dòng của ca nô là x -3 (km/h)
Vì ca nô xuôi dòng từ bến A đến bến B nên phân thức biểu thị theo x thời gian ca nô đi từ bến A đến bến B là: \(\frac{{45}}{{x + 3}}\).
b) Vì ca nô ngược dòng từ bến B đến vị trí A nên phân thức biểu thị theo x thời gian ca nô đi từ bến B đến vị trí A là: \(\frac{{45 - 27}}{{x - 3}} = \frac{{18}}{{x - 3}}\).
c) Phân thức biểu thị theo x tổng thời gian ca nô đi từ bến A đến bến B và từ bến B đến vị trí C là: \(\frac{{45}}{{x + 3}} + \frac{{18}}{{x - 3}}\).
Vì x > 3 nên x = 12 thỏa mãn điều kiện.
Nếu vận tốc của ca nô là 12km/h thì thời gian ca nô đi từ bến A đến bến B và từ bến B đến vị trí C là:
\(\frac{{45}}{{12 + 3}} + \frac{{18}}{{12 - 3}} = 5\left( h \right)\) Vậy nếu vận tốc của ca nô là 12km/h thì thời gian ca nô đi từ bến A đến bến B và từ bến B đến vị trí C là 5h.
Chứng minh \(\Delta ABD = \Delta ACD\) suy ra AB = AC.
Áp dụng định lí Pythagore để tính khoảng cách.
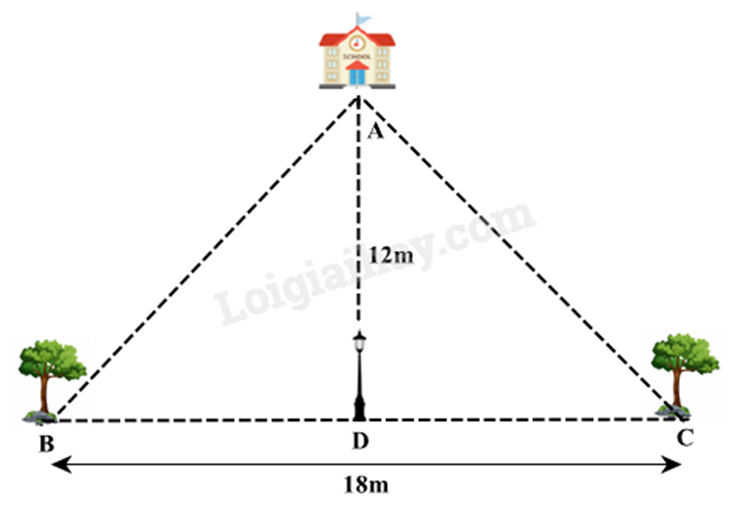
Vì hai cây B và C được trồng cách đều cột đèn D nên BD = CD = \(\frac{1}{2}\)BC = \(\frac{1}{2}\).18 = 9(m)
Vì ngôi trường A cách cột đèn D 12m theo hướng vuông góc nên \(\widehat {ADC} = {90^o}\).
Xét \(\Delta ABD\) và \(\Delta ACD\) có:
\(AD\) chung
\(\widehat {ADB} = \widehat {ADC} = \left( {{{90}^0}} \right)\)
BD = DC (cmt)
\( \Rightarrow \Delta ABD = \Delta ACD\) (hai cạnh góc vuông)
\( \Rightarrow AB = AC\)
Áp dụng định lí Pythagore vào tam giác vuông ADC, ta có:
\(\begin{array}{l}A{C^2} = A{D^2} + D{C^2} = {12^2} + {9^2} = 225\\ \Rightarrow AC = \sqrt {225} = 15\left( m \right)\end{array}\)
Vậy khoảng cách từ mỗi cây đến ngôi trường là 15m.
a) $\Delta ABH\backsim \Delta CBA$ (g.g) suy ra tỉ số các cạnh tương ứng của hai tam giác.
b) Chứng minh \(AB.AE = AC.AF = A{H^2}\) thông qua chứng minh $\Delta AHE\backsim \Delta ABH$, $\Delta AHF\backsim \Delta ACH$.
c) Dựa vào b ta có tỉ số bằng nhau. Chứng minh $\Delta AEF\backsim \Delta ACB$ (c.g.c)
d) Chứng minh $\Delta HNI\backsim \Delta HFC\Rightarrow \frac{HN}{HI}=\frac{HF}{HC}$ suy ra $\Delta HFN\backsim \Delta HCI$.
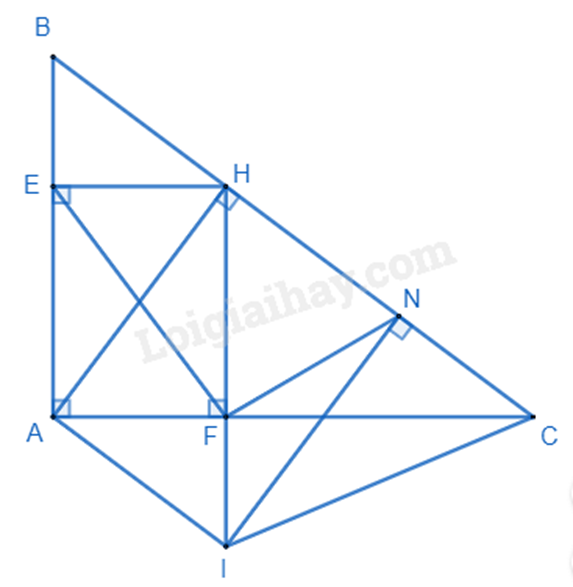
a) Xét \(\Delta ABH\) và \(\Delta CBA\) có:
\(\widehat B\) chung
\(\widehat H = \widehat A = \left( {{{90}^0}} \right)\)
$\Rightarrow \Delta ABH\backsim \Delta CBA\left( g.g \right)$ (đpcm)
\( \Rightarrow \frac{{AB}}{{BH}} = \frac{{BC}}{{AB}} \Rightarrow A{B^2} = BH.BC\) (đpcm)
b) Xét \(\Delta AHE\) và \(\Delta ABH\) có:
\(\widehat A\) chung
\(\widehat E = \widehat H\left( { = {{90}^0}} \right)\)
$\Rightarrow \Delta AHE\backsim \Delta ABH\left( g.g \right)$
\( \Rightarrow \frac{{AE}}{{AH}} = \frac{{AH}}{{AB}} \Rightarrow AE.AB = A{H^2}\) (1)
Xét \(\Delta AHF\) và \(\Delta ACH\) có:
\(\widehat A\) chung
\(\widehat F = \widehat H\left( { = {{90}^0}} \right)\)
$\Delta AHF\backsim \Delta ACH\left( g.g \right)$
\( \Rightarrow \frac{{AF}}{{AH}} = \frac{{AH}}{{AC}} \Rightarrow AF.AC = A{H^2}\) (2)
Từ (1) và (2) suy ra AE.AB = AF.AC (đpcm)
c) Theo ý b, ta có \(AE.AB = AF.AC \Rightarrow \frac{{AE}}{{AF}} = \frac{{AC}}{{AB}}\).
Xét \(\Delta AEF\) và \(\Delta ACB\) có:
\(\widehat A\) chung
\(\frac{{AE}}{{AF}} = \frac{{AC}}{{AB}}\) (cmt)
$\Rightarrow \Delta AEF\backsim \Delta ACB$ (c.g.c) (đpcm)
d) Xét \(\Delta HNI\) và \(\Delta HFC\) có:
\(\widehat H\) chung
\(\widehat N = \widehat F = \left( {{{90}^0}} \right)\)
$\Rightarrow \Delta HNI\backsim \Delta HFC\left( g.g \right)$
\( \Rightarrow \frac{{HN}}{{HI}} = \frac{{HF}}{{HC}}\)
Xét \(\Delta HFN\) và \(\Delta HCI\) có:
\(\widehat H\) chung
\(\frac{{HN}}{{HI}} = \frac{{HF}}{{HC}}\) (cmt)
$\Rightarrow \Delta HFN\backsim \Delta HCI\left( c.g.c \right)$ (đpcm)
Từ \(\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = \frac{1}{{a + b + c}}\), sử dụng quy tắc tính với phân thức, đa thức để rút gọn tìm ra a, b, c.
Theo đề bài ta có:
\(\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = \frac{1}{{a + b + c}}\)
\(\begin{array}{l}\frac{{bc + ac + ab}}{{abc}} = \frac{1}{{a + b + c}}\\\left( {bc + ac + ab} \right)\left( {a + b + c} \right) = abc\\bc\left( {a + b} \right) + b{c^2} + ac\left( {a + b} \right) + a{c^2} + ab\left( {a + b} \right) + abc - abc = 0\\bc\left( {a + b} \right) + ac\left( {a + b} \right) + ab\left( {a + b} \right) + \left( {b{c^2} + a{c^2}} \right) = 0\\bc\left( {a + b} \right) + ac\left( {a + b} \right) + ab\left( {a + b} \right) + {c^2}\left( {a + b} \right) = 0\\\left( {bc + ac + ab + {c^2}} \right)\left( {a + b} \right) = 0\\\left[ {\left( {bc + ab} \right) + \left( {ac + {c^2}} \right)} \right]\left( {a + b} \right) = 0\\\left[ {b\left( {a + c} \right) + c\left( {a + c} \right)} \right]\left( {a + b} \right) = 0\\\left( {b + c} \right)\left( {a + c} \right)\left( {a + b} \right) = 0\\ \Rightarrow \left[ \begin{array}{l}b + c = 0\\a + c = 0\\a + b = 0\end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}b = - c\\a = - c\\a = - b\end{array} \right.\end{array}\)
Trường hợp 1. Với \(b = - c\), ta có:
\(\begin{array}{l}VT = \frac{1}{{{a^{2023}}}} + \frac{1}{{{b^{2023}}}} + \frac{1}{{{c^{2023}}}}\\ = \frac{1}{{{a^{2023}}}} + \frac{1}{{{{\left( { - c} \right)}^{2023}}}} + \frac{1}{{{c^{2023}}}}\\ = \frac{1}{{{a^{2023}}}} - \frac{1}{{{c^{2023}}}} + \frac{1}{{{c^{2023}}}}\\ = \frac{1}{{{a^{2023}}}}\end{array}\)
\(\begin{array}{l}VP = \frac{1}{{{a^{2023}} + {b^{2023}} + {c^{2023}}}}\\ = \frac{1}{{{a^{2023}} + {{\left( { - c} \right)}^{2023}} + {c^{2023}}}}\\ = \frac{1}{{{a^{2023}} - {c^{2023}} + {c^{2023}}}}\\ = \frac{1}{{{a^{2023}}}}\end{array}\)
\( \Rightarrow VT = VP\) hay \(\frac{1}{{{a^{2023}}}} + \frac{1}{{{b^{2023}}}} + \frac{1}{{{c^{2023}}}} = \frac{1}{{{a^{2023}} + {b^{2023}} + {c^{2023}}}}\)
Học sinh tự chứng minh tương tự cho trường hợp \(a = - c\) và \(a = - b\) .