Giải bài 103 trang 43 sách bài tập toán 12 - Cánh diều
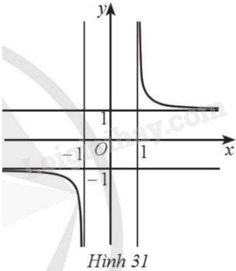
Cho hàm số \(y = f\left( x \right)\) xác định trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\), đồ thị hàm số là đường cong và có bốn đường tiệm cận như Hình 31. Căn cứ vào đồ thị hàm số: a) Viết phương trình đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số. b) Lập bảng biến thiên của hàm số.
Đề bài
Cho hàm số \(y = f\left( x \right)\) xác định trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\), đồ thị hàm số là đường cong và có bốn đường tiệm cận như Hình 31 . Căn cứ vào đồ thị hàm số:
a) Viết phương trình đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số.
b) Lập bảng biến thiên của hàm số.
Phương pháp giải - Xem chi tiết
Dựa vào đồ thị hàm số, xác định các đường tiệm cận.
Lời giải chi tiết
a) Dựa vào đồ thị hàm số ta có: \(x = 1\) và \(x = - 1\) là các đường tiệm cận đứng; \(y = 1\) và \(y = - 1\) là các đường tiệm cận ngang của đồ thị hàm số.
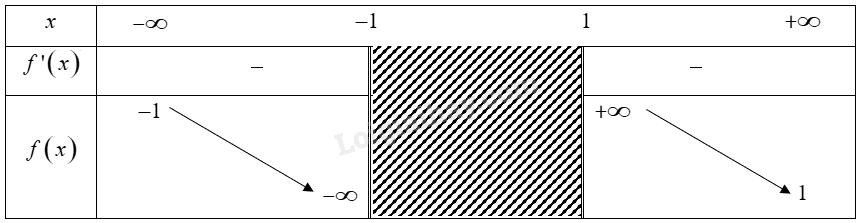
b) Bảng biến thiên của hàm số:
Cùng chủ đề:
Giải bài 103 trang 43 sách bài tập toán 12 - Cánh diều