Giải bài 104 trang 43 sách bài tập toán 12 - Cánh diều
Cho hàm số (y = fleft( x right)) xác định trên (mathbb{R}backslash left{ { - 2} right}) và có bảng biến thiên như sau: a) Tìm điểm cực đại, cực tiểu; giá trị cực đại, cực tiểu của hàm số. b) Viết phương trình đường tiệm cận đứng của đồ thị hàm số. c) Đồ thị hàm số có đường tiệm cận ngang không? Vì sao? d) Tìm công thức xác định hàm số, biết hàm số (fleft( x right)) có dạng (fleft( x right) = frac{{a{x^2} + b{rm{x}} + c}}{{x + n}})
Đề bài
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ { - 2} \right\}\) và có bảng biến thiên như sau:
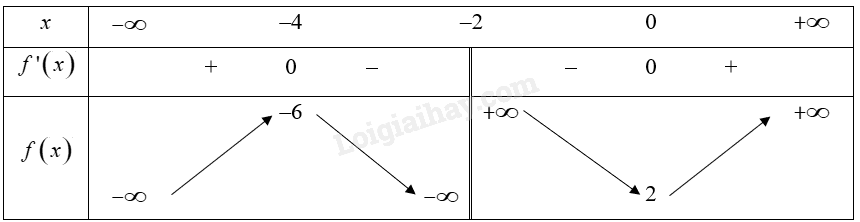
a) Tìm điểm cực đại, cực tiểu; giá trị cực đại, cực tiểu của hàm số.
b) Viết phương trình đường tiệm cận đứng của đồ thị hàm số.
c) Đồ thị hàm số có đường tiệm cận ngang không? Vì sao?
d) Tìm công thức xác định hàm số, biết hàm số \(f\left( x \right)\) có dạng \(f\left( x \right) = \frac{{a{x^2} + b{\rm{x}} + c}}{{x + n}}\)
Phương pháp giải - Xem chi tiết
‒ Dựa vào bảng biến thiên để xác định các điểm cực trị, các đường tiệm cận.
‒ Tìm tiệm cận đứng: Tính \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right)\) hoặc \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right)\), nếu một trong các giới hạn sau thoả mãn:
\(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = - \infty ;\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = - \infty \)
thì đường thẳng \(x = {x_0}\) là đường tiệm cận đứng.
‒ Tìm tiệm cận ngang: Nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\) thì đường thẳng \(y = {y_0}\) là đường tiệm cận ngang.
‒ Xác định hàm số dựa vào:
+ Xét các đường tiệm cận của đồ thị hàm số.
+ Xét các cực trị của hàm số.
+ Xét các điểm trên đồ thị hàm số.
Lời giải chi tiết
a) Dựa vào bảng biến thiên ta có:
+ Hàm số đạt cực đại tại \(x = - 4\). Khi đó giá trị cực đại \({y_{CĐ}} = -6\).
+ Hàm số đạt cực tiểu tại \(x = 0\). Khi đó giá trị cực đại \({y_{CT}} = 2\).
b) Dựa vào bảng biến thiên ta có: \(\mathop {\lim }\limits_{x \to - {2^ - }} f\left( x \right) = - \infty ;\mathop {\lim }\limits_{x \to - {2^ + }} f\left( x \right) = + \infty \).
Vậy \(x = - 2\) là tiệm cận đứng của đồ thị hàm số đã cho.
c) Dựa vào bảng biến thiên ta có: \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - \infty \).
Vậy đồ thị hàm số không có tiệm cận ngang.
d) Đồ thị hàm số có \(x = - 2\) là tiệm cận đứng. Vậy \( - \frac{n}{1} = - 2 \Leftrightarrow n = 2\).
Đồ thị hàm số đi qua điểm \(\left( {0;2} \right)\) nên ta có: \(\frac{{a{{.0}^2} + b.0 + c}}{{0 + 2}} = 2 \Leftrightarrow c = 4\).
\(f'(x) = \frac{{(a{x^2} + bx + 4)'(x + 2) - (a{x^2} + bx + 4)(x + 2)'}}{{(x + 2)'}}\)
\( = \frac{{(2ax + b)(x + n) - (a{x^2} + bx + 4)}}{{{{(x + 2)}^2}}} = \frac{{a{x^2} + 4ax + 2b - 4}}{{{{(x + 2)}^2}}}\)
\(x = 0\) là điểm cực tiểu của đồ thị hàm số nên ta có: \(\frac{{a{{.0}^2} + 4{\rm{a}}.0 + 2b - 4}}{{{{\left( {0 + 2} \right)}^2}}} = 0 \Leftrightarrow b = 2\)
Đồ thị hàm số đi qua điểm \(\left( { - 4; - 6} \right)\) nên ta có: \(\frac{{a.{{\left( { - 4} \right)}^2} + 2.\left( { - 4} \right) + 4}}{{\left( { - 4} \right) + 2}} = - 6 \Leftrightarrow a = 1\).
Vậy hàm số cần tìm là: \(y = f\left( x \right) = \frac{{{x^2} + 2{\rm{x}} + 4}}{{{\rm{x}} + 2}}\).