Giải bài 102 trang 43 sách bài tập toán 12 - Cánh diều
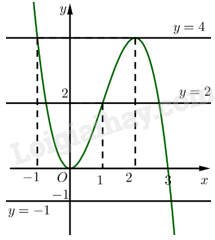
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Cho hàm số bậc ba (y = fleft( x right) = a{x^3} + b{x^2} + cx + d) có đồ thị là đường cong như Hình 30. a) Phương trình (fleft( x right) = 4) có hai nghiệm (x = - 1,x = 2). b) Phương trình (fleft( x right) = - 1) có hai nghiệm. c) Phương trình (fleft( x right) = 2) có ba nghiệm. d) Phương trình (fleft( {fleft( x right)} right) = 4) có sáu nghiệm.
Đề bài
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S).
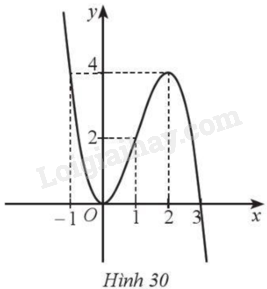
Cho hàm số bậc ba \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị là đường cong như Hình 30 .
a) Phương trình \(f\left( x \right) = 4\) có hai nghiệm \(x = - 1,x = 2\).
b) Phương trình \(f\left( x \right) = - 1\) có hai nghiệm.
c) Phương trình \(f\left( x \right) = 2\) có ba nghiệm.
d) Phương trình \(f\left( {f\left( x \right)} \right) = 4\) có sáu nghiệm.
Phương pháp giải - Xem chi tiết
‒ Xét đồ thị hàm số.
Lời giải chi tiết
• Đường thẳng \(y = 4\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại hai điểm có hoành độ bằng ‒1 và 2 nên phương trình \(f\left( x \right) = 4\) có hai nghiệm \(x = - 1,x = 2\). Vậy a) đúng.
• Đường thẳng \(y = - 1\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại một điểm nên phương trình \(f\left( x \right) = - 1\) có một nghiệm. Vậy b) sai.
Đường thẳng \(y = 2\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại ba điểm nên phương trình \(f\left( x \right) = 2\) có ba nghiệm. Vậy c) đúng.
• Ta có: \(f\left( {f\left( x \right)} \right) = 4\) khi \(f\left( x \right) = - 1\) hoặc \(f\left( x \right) = 2\).
Với \(f\left( x \right) = - 1\), phương trình có một nghiệm.
Với \(f\left( x \right) = 2\), phương trình có ba nghiệm phân biệt. Vậy phương trình đã cho có bốn nghiệm phân biệt. Vậy d) sai.
a) Đ.
b) S.
c) Đ.
d) S.