Giải bài 11 trang 106 sách bài tập toán 9 - Cánh diều tập 1 — Không quảng cáo

Đề bài

Cho đường thẳng a và điểm O với khoảng cách từ điểm O đến đường thẳng a là 1 cm. Vẽ đường tròn tâm O bán kính 3 cm.

a) Xác định vị trí tương đối của đường thẳng a và đường tròn (O).

b) Gọi A và B là các giao điểm của đường thẳng a và đường tròn (O). Tính độ dài đoạn thẳng AB.

Lời giải chi tiết

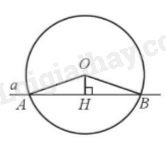
a) Kẻ $OH \bot a$ tại H, khi đó ta có $OH = 1$cm, suy ra $OH < R$ (vì $R = 3$cm). Vậy a và (O) cắt nhau.

b) Xét tam giác BOA cân tại O ($OB = OA = R$) có đường cao OH (do $OH \bot AB$) đồng thời là đường trung tuyến nên $AH = HB = \frac{{AB}}{2}$  hay $AB = 2AH$.

Áp dụng định lý Pythagore trong tam giác vuông OAH ta có:

$AH = \sqrt {O{A^2} - O{H^2}}  = \sqrt {{3^2} - {1^2}}  = 2\sqrt 2$cm.

Vậy $AB = 2AH = 2.2\sqrt 2  = 4\sqrt 2$cm.