Giải bài 11 trang 86 sách bài tập toán 9 - Cánh diều tập 2
Cho tam giác ABC vuông cân tại C và nội tiếp đường tròn (O; R). E là điểm tuỳ ý trên cung nhỏ AC của đường tròn đó. Gọi F là giao điểm của EB và CO, I là tâm đường tròn ngoại tiếp tam giác ECF. Chứng minh rằng khi E di chuyển trên cung nhỏ AC thì I luôn di chuyển trên một đoạn thẳng cố định.
Đề bài
Cho tam giác ABC vuông cân tại C và nội tiếp đường tròn (O; R). E là điểm tuỳ ý trên cung nhỏ AC của đường tròn đó. Gọi F là giao điểm của EB và CO, I là tâm đường tròn ngoại tiếp tam giác ECF. Chứng minh rằng khi E di chuyển trên cung nhỏ AC thì I luôn di chuyển trên một đoạn thẳng cố định.
Phương pháp giải - Xem chi tiết
Chứng minh \(\widehat {CEB} = \widehat {CAB} = {45^o}\) . Sau đó chứng minh tam giác ICF vuông cân tại I để suy ra I nằm trên AC.
Lời giải chi tiết
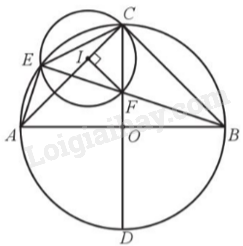
Ta có \(\widehat {CEB} = \widehat {CAB} = {45^o}\)(hai góc nội tiếp cùng chắn cung CB của đường tròn (O)). Mặt khác, I là tâm đường tròn ngoại tiếp tam giác ECF, do đó \(\widehat {CIF} = 2.\widehat {CEF} = {90^o}\). Mà IC = IF suy ra tam giác ICF vuông cân tại I, do đó \(\widehat {ICF} = {45^o}\). Lại có \(\widehat {ACO} = {45^o}\), suy ra I nằm trên AC. Vậy khi E di chuyển trên đoạn thẳng AC cố định.