Giải bài 15 trang 67 sách bài tập toán 12 - Cánh diều
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Trong không gian với hệ toạ độ (Oxyz), cho hình hộp (ABCD.A'B'C'D') có (A'left( {1;0;1} right),)(B'left( {2;1;2} right),D'left( {1; - 1;1} right),Cleft( {4;5; - 5} right)). a) Toạ độ của vectơ (overrightarrow {A'D'} ) là (left( {0; - 1;0} right)). b) Gọi toạ độ của điểm (B) là (left( {{x_B};{y_B};{z_B}} right)), ta có toạ độ của vectơ (overrightarrow {BC} ) là (left( {{x_B} - 4;{y_B} - 5;{z_B
Đề bài
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Trong không gian với hệ toạ độ \(Oxyz\), cho hình hộp \(ABCD.A'B'C'D'\) có \(A'\left( {1;0;1} \right),\)\(B'\left( {2;1;2} \right),D'\left( {1; - 1;1} \right),C\left( {4;5; - 5} \right)\). a) Toạ độ của vectơ \(\overrightarrow {A'D'} \) là \(\left( {0; - 1;0} \right)\). b) Gọi toạ độ của điểm \(B\) là \(\left( {{x_B};{y_B};{z_B}} \right)\), ta có toạ độ của vectơ \(\overrightarrow {BC} \) là \(\left( {{x_B} - 4;{y_B} - 5;{z_B} + 5} \right)\). c) Trong hình hộp \(ABCD.A'B'C'D'\), ta có: \(\overrightarrow {BC} = \overrightarrow {A'D'} \). d) Toạ độ điểm \(B\) là \(\left( {4;4; - 5} \right)\).
Phương pháp giải - Xem chi tiết
‒ Sử dụng toạ độ của vectơ \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right)\).
‒ Sử dụng tính chất hai vectơ bằng nhau: Với \(\overrightarrow u = \left( {{x_1};{y_1};{z_1}} \right)\) và \(\overrightarrow v = \left( {{x_2};{y_2};{z_2}} \right)\), ta có: \(\overrightarrow u = \overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}{x_1} = {x_2}\\{y_1} = {y_2}\\{z_1} = {z_2}\end{array} \right.\).
Lời giải chi tiết
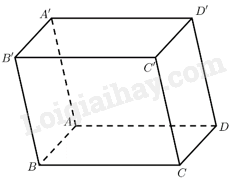
\(\overrightarrow {A'D'} = \left( {1 - 1; - 1 - 0;1 - 1} \right) = \left( {0; - 1;0} \right)\). Vậy a) đúng.
\(\overrightarrow {BC} = \left( {4 - {x_B};5 - {y_B}; - 5 - {z_B}} \right)\). Vậy b) sai.
\(ABCD.A'B'C'D'\) là hình hộp nên \(\overrightarrow {BC} = \overrightarrow {A'D'} \). Vậy c) đúng.
Ta có: \(\overrightarrow {BC} = \overrightarrow {A'D'} \Leftrightarrow \left\{ \begin{array}{l}4 - {x_B} = 0\\5 - {y_B} = - 1\\ - 5 - {z_B} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 4\\{y_B} = 6\\{z_B} = - 5\end{array} \right.\). Vậy \(B\left( {4;6; - 5} \right)\). Vậy d) sai.
a) Đ
b) S
c) Đ
d) S