Giải bài 15 trang 85 sách bài tập toán 9 - Cánh diều tập 1
Cho tam giác ABC vuông tại A. Chứng minh \(\tan \frac{{\widehat B}}{2} = \frac{{AC}}{{AB + BC}}\)
Đề bài
Cho tam giác ABC vuông tại A. Chứng minh \(\tan \frac{{\widehat B}}{2} = \frac{{AC}}{{AB + BC}}\)
Phương pháp giải - Xem chi tiết
Bước 1: Kẻ đường phân giác BD.
Bước 2: Áp dụng tỉ số lượng giác trong tam giác vuông ABD: \(\tan {B_1} = \frac{{AD}}{{AB}}\).
Bước 3: Áp dụng tính chất đường phân giác trong tam giác suy ra \(\frac{{AD}}{{AB}} = \frac{{CD}}{{BC}}\).
Bước 4: Áp dụng tính chất dãy tỉ số bằng nhau:\(\frac{{AD}}{{AB}} = \frac{{CD}}{{BC}} = \frac{{AD + CD}}{{AB + BC}} = \frac{{AC}}{{AB + BC}}\)
Lời giải chi tiết
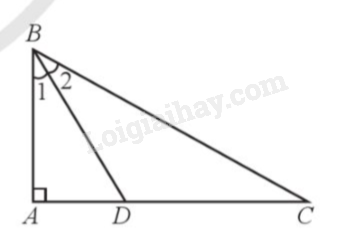
Kẻ đường phân giác BD của tam giác ABC. Khi đó ta có \(\widehat {{B_1}} = \widehat {{B_2}} = \frac{{\widehat B}}{2}\).
Vì tam giác ABD vuông tại A, ta có \(\tan {B_1} = \frac{{AD}}{{AB}}\)(1)
Mà AD là đường phân giác của tam giác ABC nên ta có \(\frac{{AD}}{{CD}} = \frac{{AB}}{{BC}}\), suy ra \(\frac{{AD}}{{AB}} = \frac{{CD}}{{BC}}\).
Do đó \(\frac{{AD}}{{AB}} = \frac{{CD}}{{BC}} = \frac{{AD + CD}}{{AB + BC}} = \frac{{AC}}{{AB + BC}}\) (2)
Từ (1) và (2) ta có \(\tan {B_1} = \tan \frac{{\widehat B}}{2} = \frac{{AD}}{{AB}} = \frac{{AC}}{{AB + BC}}\).