Giải bài 15 trang 111 sách bài tập toán 9 - Cánh diều tập 2
Cho hình vuông ABCD với tâm O. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AD, DC, CB, BA (Hình 15). a) Chứng minh tứ giác MNPQ là hình vuông. b) Phép quay ngược chiều 90° tâm O biến các điểm O, D, N tương ứng thành các điểm nào? c) Chỉ ra các phép quay tâm O giữ nguyên hình vuông MNPQ.
Đề bài
Cho hình vuông ABCD với tâm O. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AD, DC, CB, BA (Hình 15).
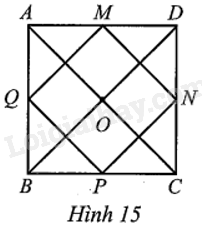
a) Chứng minh tứ giác MNPQ là hình vuông.
b) Phép quay ngược chiều 90° tâm O biến các điểm O, D, N tương ứng thành các điểm nào?
c) Chỉ ra các phép quay tâm O giữ nguyên hình vuông MNPQ.
Phương pháp giải - Xem chi tiết
Chứng minh MN = MQ và MN ⊥ MQ để suy ra MNPQ là hình vuông
Dựa vào phép quay thuận chiều \({\alpha ^o}\) (\({0^o} < {\alpha ^o} < {360^o}\)) tâm O giữ nguyên điểm O, biến điểm M (khác điểm O) thành điểm M’ thuộc đường tròn (O; OM) sao cho tia OM quay thuận chiều kim đồng hồ đến tia OM’ thì điểm M tạo nên cung MnM’ có số đo \({\alpha ^o}\).
Dựa vào phép quay thuận chiều \({\alpha ^o}\) (\({0^o} < {\alpha ^o} < {360^o}\)) tâm O được phát biểu tương tự như trên.
Lời giải chi tiết
a) Xét ∆ABC có Q, P lần lượt là trung điểm của AB, BC nên QP là đường trung bình của tam giác, do đó QP // AC và \(QP = \frac{1}{2}AC\).
Tương tự, ta có: MN là đường trung bình của tam giác ACD, do đó MN // AC và \(MN = \frac{1}{2}AC\).
Do đó MNPQ là hình bình hành.
Mặt khác, ta cũng chứng minh được MQ là đường trung bình của ∆ABD nên
\(MQ = \frac{1}{2}BD\).
Lại có ABCD là hình vuông nên AC = BD và AC ⊥ BD.
Suy ra MN = MQ và MN ⊥ MQ.
Khi đó hình bình hành MNPQ là hình vuông.
b) Phép quay ngược chiều 90° tâm O biến điểm O tương ứng thành chính nó.
Do ABCD là hình vuông tâm O nên OA = OB = OC = OD.
Theo câu a, ta có \(\widehat {AOD} = {90^o}\).
Do đó, tia OD quay ngược chiều 90° tâm O đến tia OA.
Tương tự, đối với hình vuông MNPQ ta cũng có ON = OM và \(\widehat {NOM} = {90^o}\)nên tia ON quay ngược chiều 90° tâm O đến tia OM.
Vậy phép quay ngược chiều 90° tâm O biến các điểm O, D, N tương ứng thành các điểm O, A, M.
c) Các phép quay tâm O giữ nguyên hình vuông MNPQ là các phép quay thuận chiều α° tâm O và các phép quay ngược chiều α° tâm O, với α° lần lượt nhận các giá trị:
α 1 ° = 90°; α 2 ° = 180°; α 3 ° = 270°; α 4 ° = 360°.