Giải bài 16 trang 100 sách bài tập toán 11 - Cánh diều — Không quảng cáo

Đề bài

Cho tứ diện $ABCD$. Gọi $M$, $N$ lần lượt là trung điểm của các cạnh $AB$, $AD$ và $P$ là một điểm nằm trên $CD$. Đường thẳng $BC$ cắt mặt phẳng $\left( {MNP} \right)$ tại $Q$. Chứng minh rằng $PQ\parallel BD$.

Lời giải chi tiết

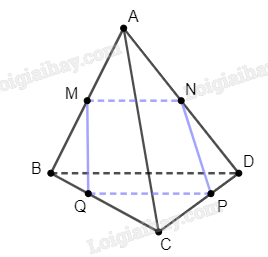
Ta có $M$ là trung điểm của $AB$, $N$ là trung điểm của $AD$, nên $MN$ là đường trung bình của tam giác $ABD$. Suy ra $MN\parallel BD$.

Xét ba mặt phẳng $\left( {MNP} \right)$, $\left( {ABD} \right)$ và $\left( {BCD} \right)$, ta có $MN$ là giao tuyến của $\left( {ABD} \right)$ và $\left( {MNP} \right)$; $PQ$ là giao tuyến của $\left( {BCD} \right)$ và $\left( {MNP} \right)$, $BD$ là giao tuyến của $\left( {ABD} \right)$ và $\left( {BCD} \right)$.

Mà $MN\parallel BD$, nên theo định lí về giao tuyến của ba mặt phẳng, ta suy ra $PQ\parallel BD$.

Bài toán được chứng minh.