Giải bài 17 trang 95 sách bài tập toán 11 - Cánh diều
Cho tam giác ABC và các điểm M, N, P
Đề bài
Cho tam giác ABC và các điểm M, N, P đôi một phân biệt thoả mãn MA = MB = MC, NA = NB = NC, PA = PB = PC. Chứng minh rằng M, N, P thẳng hàng.
Phương pháp giải - Xem chi tiết
Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
Lời giải chi tiết
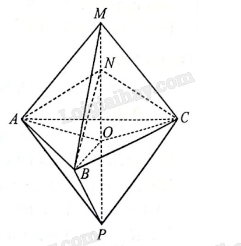
Gọi O là tâm đường tròn ngoại tiếp của tam giác ABC.
Giả sử ba điểm M, N, P đều không thuộc mặt phẳng (ABC).
Áp dụng kết quả Bài 16 cho ba hình chóp M.ABC, N.ABC, P.ABC ta có \(MO \bot \left( {ABC} \right),{\rm{ }}NO \bot \left( {ABC} \right),{\rm{ }}PO \bot \left( {ABC} \right).\)Do đó ba đường thẳng MO, NO, PO trùng nhau hay M, N, P thẳng hàng.
Giả sử trong ba điểm M, N, P có một điểm nằm trên (ABC). Khi đó, theo giả thiết ta có điểm đó trùng O. Như vậy, cùng với kết quả trên ta có ba điểm M, N, P thẳng hàng.