Giải bài 2.47 trang 57 sách bài tập toán 12 - Kết nối tri thức
Trên phần mềm GeoGebra 3D với các trục tọa độ được dựng sẵn, bạn Minh vẽ hai hình hộp chữ nhật với một số cạnh đặt dọc theo các trục tọa độ. Ba đỉnh thuộc mặt dưới của hình hộp thứ nhất lần lượt là (Oleft( {0;0;0} right)), (Aleft( {2;0;0} right)), (Bleft( {0;3;0} right)). Biết hình hộp thứ hai ở vị trí cao hơn hình hộp thứ nhất là 5 đơn vị, xác định tọa độ của các đỉnh (O',A',B') thuộc mặt dưới của hình hộp thứ hai.
Đề bài
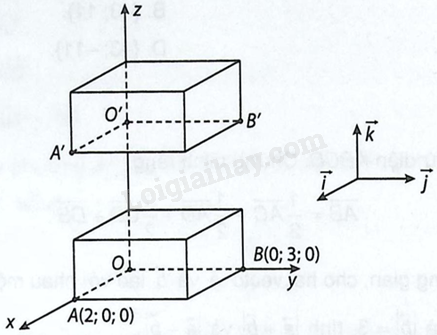
Trên phần mềm GeoGebra 3D với các trục tọa độ được dựng sẵn, bạn Minh vẽ hai hình hộp chữ nhật với một số cạnh đặt dọc theo các trục tọa độ. Ba đỉnh thuộc mặt dưới của hình hộp thứ nhất lần lượt là \(O\left( {0;0;0} \right)\), \(A\left( {2;0;0} \right)\), \(B\left( {0;3;0} \right)\). Biết hình hộp thứ hai ở vị trí cao hơn hình hộp thứ nhất là 5 đơn vị, xác định tọa độ của các đỉnh \(O',A',B'\) thuộc mặt dưới của hình hộp thứ hai.
Phương pháp giải - Xem chi tiết
Sử dụng tính chất của hình hộp chữ nhật trong đề để tìm ra các vectơ bằng nhau phù hợp,
sau đó tính toán để tìm tọa độ các điểm.
Lời giải chi tiết
Vì hình hộp thứ hai nằm ngay phía trên hình hộp thứ nhất và cách hình hộp thứ nhất 5 đơn vị nên \(\overrightarrow {OO'} ,\overrightarrow {AA'} ,\overrightarrow {BB'} \) cùng hướng với \(\overrightarrow k \) và có độ dài là 5.
Suy ra \(\overrightarrow {OO'} = \overrightarrow {AA'} = \overrightarrow {BB'} = \left( {0;0;5} \right)\) do đó \(O'\left( {0;0;5} \right)\), \(A'\left( {2;0;5} \right)\) và \(B'\left( {0;3;5} \right)\).