Giải bài 24 trang 97 sách bài tập toán 8 - Cánh diều
Cho tam giác \(ABC\) cân tại \(A\) có các đường trung tuyến \(BM,CN\) cắt nhau tại \(G\)
Đề bài
Cho tam giác \(ABC\) cân tại \(A\) có các đường trung tuyến \(BM,CN\) cắt nhau tại \(G\). Trên tia đối của tia \(GB,GC\) lần lượt lấy các điểm \(D,E\) sao cho \(GD = GB,GE = GC\). Tứ giác \(BEDC\) là hình gì? Vì sao?
Phương pháp giải - Xem chi tiết
Dựa vào tính chất và dấu hiệu nhận biết của hình bình hành và hình chữ nhật để xác định tứ giác \(BEDC\) .
Lời giải chi tiết
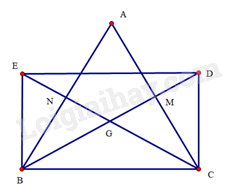
Tứ giác \(BEDC\) có hai đường chéo \(BD\) và \(CE\) cắt nhau tại trung điểm \(G\) của mỗi đường nên \(BEDC\) là hình bình hành.
Ta có: \(AB = AC,AM = CM,AN = BN\) nên \(BN = CM\).
\(\Delta BCM = \Delta CBN\) (c.g.c). Suy ra \(BM = CN\).
Do \(G\) là trọng tâm của tam giác \(ABC\) nên
\(BG = \frac{2}{3}BM\) và \(CG = \frac{2}{3}CN\)
Do đó \(BG = CG\). Mà \(G\) là trung điểm của \(BD\) và \(CE\), suy ra \(BD = CE\)
Hình bình hành \(BEDC\) có \(BD = CE\) nên \(BEDC\) là hình chữ nhật.