Giải bài 4 trang 55 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho hình chóp S.ABCD có đáy là hình thoi, O là giao điểm của hai đường chéo, \(SA = SC,SB = SD\).
Đề bài
Cho hình chóp S.ABCD có đáy là hình thoi, O là giao điểm của hai đường chéo, \(SA = SC,SB = SD\).
a) Chứng minh rằng \(SO \bot \left( {ABCD} \right)\).
b) Gọi I, J lần lượt là trung điểm của BA, BC. Chứng minh rằng \(IJ \bot \left( {SBD} \right)\).
c) Chứng minh rằng \(BD \bot \left( {SAC} \right)\).
Phương pháp giải - Xem chi tiết
a, c) Sử dụng kiến thức về định lí đường thẳng vuông góc với mặt phẳng để chứng minh: Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\).
b) Sử dụng kiến thức về liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng: Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
Lời giải chi tiết
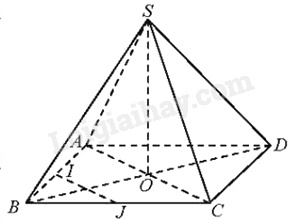
a) Vì ABCD là hình thoi tâm O nên O là trung điểm của AC, O là trung điểm của BD.
Vì \(SA = SC\) nên tam giác SAC cân tại S. Do đó, SO là đường trung tuyến đồng thời là đường cao của tam giác SAC. Do đó, \(SO \bot AC\)
Vì \(SB = SD\) nên tam giác SBD cân tại S. Do đó, SO là đường trung tuyến đồng thời là đường cao của tam giác SBD. Do đó, \(SO \bot BD\)
Vì \(SO \bot AC\), \(SO \bot BD\), AC và BD cắt nhau và nằm trong (ABCD).
Do đó, \(SO \bot \left( {ABCD} \right)\)
b) Vì \(SO \bot AC,BD \bot AC\) (do ABCD là hình thoi tâm), SO và BD cắt nhau tại O và nằm trong (SBD) nên \(AC \bot \left( {SBD} \right)\) (1)
Vì I, J lần lượt là trung điểm của BA, BC nên IJ là đường trung bình của tam giác BAC. Do đó, IJ//AC (2)
Từ (1) và (2) suy ra: \(IJ \bot \left( {SBD} \right)\).
c) Vì \(SO \bot BD,BD \bot AC\), SO và AC cắt nhau tại O và nằm trong (SAC) nên \(BD \bot \left( {SAC} \right)\).