Giải bài 5 trang 72 SGK Toán 8 – Chân trời sáng tạo
Tứ giác nào trong Hình 15 là hình thang cân?
Đề bài
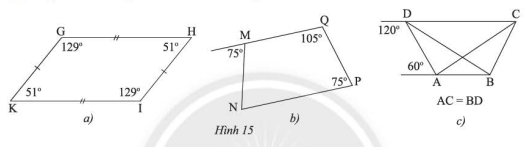
Tứ giác nào trong Hình 15 là hình thang cân?
Phương pháp giải - Xem chi tiết
Sử dụng dấu hiệu nhận biết hình thang cân
Lời giải chi tiết
a) Xét tứ giác \(KGHI\) ta có:
\(\widehat {{\rm{HGK}}} + \widehat {{\rm{GKI}}} = 129^\circ + 51^\circ = 180^\circ \)
Mà hai góc ở vị trí trong cùng phía
Suy ra \(GH\;{\rm{//}}\;KI\)
Suy ra \(KGHI\) là hình thang
b)
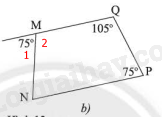
Ta có:
\(\widehat {M_1} + \widehat {M_2} = 180^0\) (hai góc kề bù)
\(\Rightarrow \widehat{M_2} = 180^0 - \widehat{M_1} = 180^0 - 75^0 = 105^0\)
Xét tứ giác MNPQ có: \(\widehat {M_2} + \widehat N + \widehat P + \widehat Q = 360^0 \Rightarrow \widehat N = 360^0 - \widehat {M_2} - \widehat P - \widehat Q = 360^0 - 105^0 - 75^0 - 105^0 = 75^0\)
Ta có: \(\widehat {M_1} = \widehat N = 75^0\) mà \(\widehat {M_1}\) và \( \widehat N\) ở vị trí so le trong nên MQ //NP suy ra MNPQ là hình thang.
Mà \(\widehat {M_2} = \widehat Q = 105^0; \widehat {N} = \widehat P = 75^0\)
Suy ra \(MNPQ\) là hình thang cân
c)
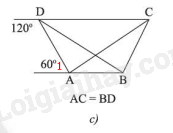
Ta có:
\(\widehat {{\rm{ADC}}} = 180^\circ - 120^\circ = 60^\circ \)
Ta có: \(\widehat {{\rm{ADC}}} = \widehat {{A_1}} = 60^\circ \)
Mà hai góc ở vị trí so le trong
Suy ra \(AB\) // \(CD\)
Suy ra \(ABCD\) là hình thang
Mà \(AC = BD\)
Suy ra \(ABCD\) là hình thang cân