Giải bài 5 trang 96 vở thực hành Toán 9 tập 2
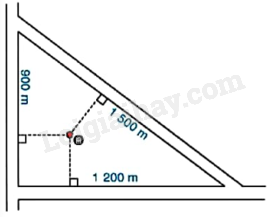
Người ta vẽ bản quy hoạch của một khu dân cư được bao xung quanh bởi ba con đường thẳng lập thành một tam giác với độ dài các cạnh là 900m, 1 200m và 1 500m như hình vẽ dưới đây. a) Tính chu vi và diện tích của phần đất giới hạn bởi tam giác trên. b) Họ muốn xây dựng một khách sạn bên trong khu dân cư cách đều cả ba con đường đó. Hỏi khi đó khách sạn sẽ cách mỗi con đường một khoảng là bao nhiêu?
Đề bài
Người ta vẽ bản quy hoạch của một khu dân cư được bao xung quanh bởi ba con đường thẳng lập thành một tam giác với độ dài các cạnh là 900m, 1 200m và 1 500m như hình vẽ dưới đây.
a) Tính chu vi và diện tích của phần đất giới hạn bởi tam giác trên.
b) Họ muốn xây dựng một khách sạn bên trong khu dân cư cách đều cả ba con đường đó. Hỏi khi đó khách sạn sẽ cách mỗi con đường một khoảng là bao nhiêu?
Phương pháp giải - Xem chi tiết
a) + Chu vi phần đất giới hạn bởi tam giác trên là tổng của ba cạnh tam giác.
+ Chứng minh phần đất giới hạn bởi tam giác là tam giác vuông.
+ Khi đó, diện tích phần đất giới hạn bởi tam giác đó bằng nửa tích hai cạnh góc vuông.
b) + Để khách sạn cách đều ba con đường thì cần phải được xây dựng vào đúng vị trí tâm đường tròn nội tiếp của tam giác ABC.
+ Chiều cao hạ từ đỉnh I xuống các cạnh BC, CA, AB của các tam giác IBC, ICA, IAB đều bằng bán kính r của đường tròn nội tiếp tam giác ABC.
+ Ta có: \({S_{ABC}} = {S_{IBC}} + {S_{ICA}} + {S_{IAB}} \) \( = \frac{1}{2}r.\left( {AB + AC + BC} \right) = \frac{{r.C}}{2}\), tính được r.
Lời giải chi tiết
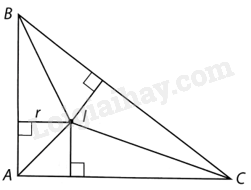
a) Phần đất cần tính diện tích có dạng hình một tam giác ABC, với \(AB = 900m,AC = 1\;200m,BC = 1\;500m\).
Ta thấy \(B{C^2} = A{B^2} + A{C^2}\) . Do vậy, theo định lí Pythagore đảo thì ABC là tam giác vuông tại A.
Chu vi và diện tích của tam giác ABC lần lượt là: \(C = AB + AC + BC = 3\;600m\); \({S_{ABC}} = \frac{1}{2}.AB.AC = 540\;000{m^2}\)
b) Để khách sạn cách đều cả ba con đường thì cần phải được xây dựng vào đúng vị trí tâm đường tròn nội tiếp của tam giác ABC. Khi đó, cho chiều cao hạ từ đỉnh I xuống các cạnh BC, CA, AB của các tam giác IBC, ICA, IAB đều bằng bán kính r của đường tròn nội tiếp tam giác ABC. Do đó
\({S_{ABC}} = {S_{IBC}} + {S_{ICA}} + {S_{IAB}} \\= \frac{1}{2}r.\left( {AB + AC + BC} \right) = \frac{{r.C}}{2}.\)
Suy ra: \(r = \frac{{2.{S_{ABC}}}}{C} = 300m\). Vậy khách sạn sẽ cách mỗi con đường là 300m.