Giải bài 5 trang 97 sách bài tập toán 12 - Chân trời sáng tạo
Kết quả khảo sát cân nặng của 80 con tôm càng xanh 5 tháng tuổi ở một khu nuôi tôm được biểu diễn ở biểu đồ tần số dưới đây. a) Hãy lập bảng tần số ghép nhóm cho mẫu số liệu trên. b) Hãy tìm khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.
Đề bài
Kết quả khảo sát cân nặng của 80 con tôm càng xanh 5 tháng tuổi ở một khu nuôi tôm được biểu diễn ở biểu đồ tần số dưới đây.
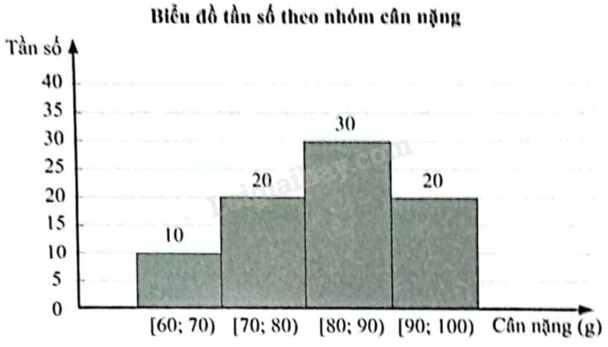
a) Hãy lập bảng tần số ghép nhóm cho mẫu số liệu trên.
b) Hãy tìm khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.
Phương pháp giải - Xem chi tiết
‒ Sử dụng công thức tính khoảng biến thiên của mẫu số liệu ghép nhóm: \(R = {a_{m + 1}} - {a_1}\).
‒ Sử dụng công thức tính các tứ phân vị của mẫu số liệu ghép nhóm:
Tứ phân vị thứ \(k\) được xác định như sau: \({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} - C}}{{{n_m}}}\left( {{u_{m + 1}} - {u_m}} \right)\)
trong đó:
• \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu;
• \(\left[ {{u_m};{u_{m + 1}}} \right)\) là nhóm chứa tứ phân vị thứ \(k\);
• \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ \(k\);
• \(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
‒ Sử dụng công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm: \(\Delta Q = {Q_3} - {Q_1
Lời giải chi tiết
a) Bảng tần số ghép nhóm:

b) Khoảng biến thiên của mẫu số liệu ghép nhóm đó là: \(R = 100 - 60 = 40\) (g).
Gọi \({x_1};{x_2};...;{x_{80}}\) là mẫu số liệu gốc gồm cân nặng của 80 con tôm càng xanh 5 tháng tuổi theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_{20}} + {x_{21}}} \right) \in \left[ {70;80} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_1} = 70 + \frac{{\frac{{1.80}}{4} - 10}}{{20}}\left( {80 - 70} \right) = 75\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_{60}} + {x_{61}}} \right) \in \left[ {90;100} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_3} = 90 + \frac{{\frac{{3.80}}{4} - \left( {10 + 20 + 30} \right)}}{{20}}\left( {100 - 90} \right) = 90\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \(\Delta Q = {Q_3} - {Q_1} = 90 - 75 = 15\) (g).