Giải bài 7.52 trang 43 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Cho hình chóp S.ABCD có \(SA \bot (ABCD)\) biết ABCD là hình vuông cạnh bằng a và \(SA = a\sqrt 2 \)
Đề bài
Cho hình chóp S.ABCD có \(SA \bot (ABCD)\) biết ABCD là hình vuông cạnh bằng a và \(SA = a\sqrt 2 \)
a) Chứng minh rằng\((SAC) \bot (SBD)\) và \((SAD) \bot (SCD)\)
b) Gọi BE, DF là hai đường cao của tam giác SBD. Chứng minh \((ACF) \bot (SBC)\) và \((AEF) \bot (SAC)\)
c) Tính theo a khoản cách giữa hai đường thẳng BD và SC
Phương pháp giải - Xem chi tiết
a) Chứng minh \(BD \bot \left( {SAC} \right)\) từ đó suy ra \(\left( {SBD} \right) \bot \left( {SAC} \right)\).
b) Chứng minh \(AF \bot \left( {SBC} \right)\) từ đó suy ra \(\left( {ACF} \right) \bot \left( {SBC} \right)\).
Chứng minh \(SC \bot \left( {AEF} \right)\) suy ra \(\left( {AEF} \right) \bot \left( {SAC} \right)\).
c) Dựng đoạn vuông góc chung của \(BD\) và \(SC\),
Tính độ dài đoạn vuông góc chung của \(BD\) và \(SC\),
Lời giải chi tiết
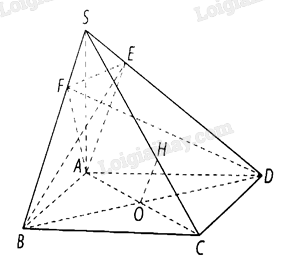
a) Ta có: \(BD \bot AC,SA \bot \left( {ABCD} \right)\) nên \(SA \bot BD\), suy ra \(BD \bot \left( {SAC} \right)\), mà mặt phẳng \(\left( {SBD} \right)\) chứa đường thẳng \(BD\), do đó \(\left( {SBD} \right) \bot \left( {SAC} \right)\).
Ta có: \(CD \bot AD,CD \bot SA\), suy ra \(CD \bot \left( {SAD} \right)\), mà mặt phẳng \(\left( {SCD} \right)\) chứa đường thẳng \(CD\), do đó \(\left( {SCD} \right) \bot \left( {SAD} \right)\).
b) Ta có: \(AD \bot \left( {SAB} \right)\) nên \(AD \bot SB\), mà \(SB \bot DF\) suy ra \(SB \bot \left( {ADF} \right)\), do đó
\(SB \bot AF\).
Ta lại có \(BC \bot \left( {SAB} \right)\) nên \(BC \bot AF\), suy ra \(AF \bot \left( {SBC} \right)\), mà mặt phẳng \(\left( {ACF} \right)\) chứa đường thẳng \(AF\) nên \(\left( {ACF} \right) \bot \left( {SBC} \right)\).
Vì \(AF \bot \left( {SBC} \right)\) nên \(AF \bot SC\).
Tương tự, ta có \(AE \bot \left( {SCD} \right)\) nên \(AE \bot SC\), suy ra \(SC \bot \left( {AEF} \right)\), mà mặt phẳng \(\left( {SAC} \right)\) chứa đường thẳng \(SC\) nên \(\left( {AEF} \right) \bot \left( {SAC} \right)\).
c) Gọi \(O\) là giao điểm của \(AC\) và \(BD\), kẻ \(OH \bot SC\) tại \(H\), mà \(BD \bot \left( {SAC} \right)\) nên \(OH \bot BD\), suy ra \(OH\) là đoạn vuông góc chung của \(BD\) và \(SC\), hay \(d\left( {BD,SC} \right) = OH\)
Ta có: \(\Delta CHO\) đồng dạng với \(\Delta CAS\) nên \(\frac{{OC}}{{CS}} = \frac{{OH}}{{AS}}\), suy ra \(OH = \frac{{AS \cdot OC}}{{CS}} = \frac{a}{2}\).
Vậy \(d\left( {BD,SC} \right) = \frac{a}{2}\).