Giải bài 9.8 trang 53 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tam giác ABC nội tiếp đường tròn (O). Biết rằng (widehat {ACB} = {50^o},widehat {ABC} = {70^o}), tính số đo các cung nhỏ $oversetfrown{BC},oversetfrown{CA},oversetfrown{AB}$ của đường tròn (O).
Đề bài
Cho tam giác ABC nội tiếp đường tròn (O). Biết rằng \(\widehat {ACB} = {50^o},\widehat {ABC} = {70^o}\), tính số đo các cung nhỏ $\overset\frown{BC},\overset\frown{CA},\overset\frown{AB}$ của đường tròn (O).
Phương pháp giải - Xem chi tiết
Trong một đường tròn, góc nội tiếp bằng nửa số đo của cung bị chắn.
Lời giải chi tiết
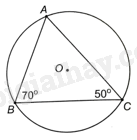
Xét (O) có:
+ Vì góc nội tiếp ACB chắn cung nhỏ AB nên sđ$\overset\frown{AB}$ nhỏ \( = 2\widehat {ACB} = {100^o}\).
+ Vì góc nội tiếp ABC chắn cung nhỏ AC nên sđ$\overset\frown{AC}$ nhỏ \( = 2\widehat {ABC} = {140^o}\).
+ Vì góc nội tiếp BAC chắn cung nhỏ BC nên sđ$\overset\frown{BC}$ nhỏ \( = 2\widehat {BAC} = 2.\left( {{{180}^o} - \widehat {ACB} - \widehat {ABC}} \right) = {120^o}\).
Cùng chủ đề:
Giải bài 9. 8 trang 53 sách bài tập toán 9 - Kết nối tri thức tập 2