Giải bài 9. 13 trang 53 sách bài tập toán 9 - Kết nối tri thức tập 2 — Không quảng cáo

Đề bài

Cho tam giác ABC vuông tại A có $AB = 4cm,AC = 6cm$. Tính bán kính của đường tròn nội tiếp tam giác ABC.

Lời giải chi tiết

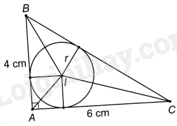
Gọi I là tâm đường tròn nội tiếp tam giác ABC, r là bán kính của đường tròn nội tiếp tam giác ABC.

Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có: $B{C^2} = A{B^2} + A{C^2} = 52$ nên $BC = 2\sqrt {13} cm$

Diện tích của tam giác ABC là: $S = \frac{1}{2}AB.AC = 12\left( {c{m^2}} \right)$.

Ta có: $S = {S_{AIB}} + {S_{AIC}} + {S_{BIC}} = \frac{1}{2}r\left( {AB + BC + CA} \right)$, suy ra: $r = \frac{{2S}}{{AB + BC + AC}} = \frac{{12}}{{5 + \sqrt {13} }}\left( {cm} \right)$.