Giải bài 9 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2 — Không quảng cáo

Đề bài

Cho hình chóp cụt tam giác đều ABC.A’B’C’ có đường cao $HH' = 2a$. Cho biết $AB = 2a,A'B' = a$. Gọi ${B_1},{C_1}$ lần lượt là trung điểm của AB, AC. Tính thể tích của:

a) Khối chóp cụt đều ABC.A’B’C’;

b) Khối lăng trụ $A{B_1}{C_1}.A'B'C'$.

Lời giải chi tiết

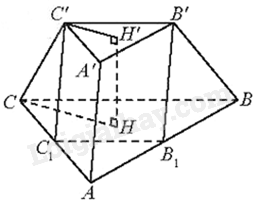
a) Vì tam giác ABC, A’B’C’ đều nên ${S_{ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 ,{S_{A'B'C'}} = \frac{{A'B{'^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}$

Do đó thể tích khối chóp cụt đều ABC.A’B’C’ là:

${{V}_{ABC.ABC}}$$=\frac{1}{3}.HH'\left( {{S}_{ABC}}+\sqrt{{{S}_{ABC}}.{{S}_{A'B'C'}}}+{{S}_{A'B'C'}} \right)$$=\frac{1}{3}.2a\left( {{a}^{2}}\sqrt{3}+\sqrt{{{a}^{2}}\sqrt{3}.\frac{{{a}^{2}}\sqrt{3}}{4}}+\frac{{{a}^{2}}\sqrt{3}}{4} \right)$

$= \frac{2}{3}a\left( {\frac{{5\sqrt 3 {a^2}}}{4} + \frac{{{a^2}\sqrt 3 }}{2}} \right) = \frac{{7{a^3}\sqrt 3 }}{6}$

b) Thể tích khối lăng trụ $A{B_1}{C_1}.A'B'C'$ là: ${V_{A{B_1}{C_1}.A'B'C'}} = HH'.{S_{A'B'C}} = 2a.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{2}$