Giải bài tập 4.16 trang 20 SGK Toán 12 tập 2 - Cùng khám phá
Một lò xo có chiều dài tự nhiên là \({l_0} = 10{\mkern 1mu} {\rm{cm}}\)(Hình 4.9a). Để kéo giãn lò xo \(x{\mkern 1mu} ({\rm{m}})\) cần một lực có độ lớn \(f(x) = kx{\mkern 1mu} ({\rm{N}})\), trong đó \(k\) là độ cứng của lò xo và có giá trị không đổi. (Hình 4.9b). a) Tìm \(k\), biết dưới tác dụng của một lực 40 N, lò xo bị giãn và chiều dài của lò xo khi ấy là \({l_1} = 15{\mkern 1mu} {\rm{cm}}\). b) Nếu một lực có độ lớn \(f(x){\mkern 1mu} ({\rm{N}})\) làm biến dạng lò xo từ độ giãn \(a{\mke
Đề bài
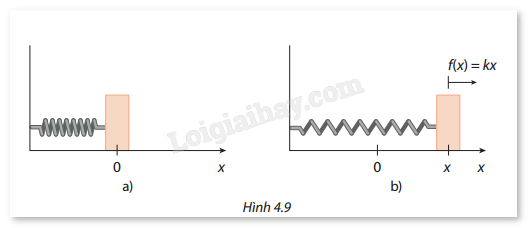
Một lò xo có chiều dài tự nhiên là \({l_0} = 10{\mkern 1mu} {\rm{cm}}\)(Hình 4.9a). Để kéo giãn lò xo \(x{\mkern 1mu} ({\rm{m}})\) cần một lực có độ lớn \(f(x) = kx{\mkern 1mu} ({\rm{N}})\), trong đó \(k\) là độ cứng của lò xo và có giá trị không đổi. (Hình 4.9b).
a) Tìm \(k\), biết dưới tác dụng của một lực 40 N, lò xo bị giãn và chiều dài của lò xo khi ấy là \({l_1} = 15{\mkern 1mu} {\rm{cm}}\).
b) Nếu một lực có độ lớn \(f(x){\mkern 1mu} ({\rm{N}})\) làm biến dạng lò xo từ độ giãn \(a{\mkern 1mu} ({\rm{m}})\) đến \(b{\mkern 1mu} ({\rm{m}})\) thì công của lực đó được cho bởi công thức \(A = \int_a^b f (x){\mkern 1mu} dx\)(J). Tính công của một lực làm lò xo biến dạng từ chiều dài 15 cm đến 18 cm.
Phương pháp giải - Xem chi tiết
a)
- Sử dụng định luật Hooke: \(f(x) = kx\).
- Tìm độ giãn của lò xo: \(x = {l_1} - {l_0}\).
- Suy ra \(k\) từ công thức \(f(x) = kx\) với \(f(x) = 40{\mkern 1mu} {\rm{N}}\).
b)
- Sử dụng công thức công của lực: \(A = \int_a^b f (x){\mkern 1mu} dx\).
- Biểu thức lực \(f(x) = kx\) được thay vào công thức tích phân để tính công.
- Tính công khi lò xo giãn từ \(a = {l_1} - {l_0}\) đến \(b = {l_2} - {l_0}\) (trong đó \({l_2} = 18{\mkern 1mu} {\rm{cm}}\)).
Lời giải chi tiết
a)
- Độ giãn của lò xo khi chịu lực 40 N là:
\(x = {l_1} - {l_0} = 15{\mkern 1mu} {\rm{cm}} - 10{\mkern 1mu} {\rm{cm}} = 5{\mkern 1mu} {\rm{cm}} = 0.05{\mkern 1mu} {\rm{m}}\)
- Áp dụng định luật Hooke \(f(x) = kx\), ta có:
\(40 = k \times 0.05\)
Suy ra độ cứng của lò xo \(k\):
\(k = \frac{{40}}{{0.05}} = 800{\mkern 1mu} {\rm{N/m}}\)
b)
- Độ giãn khi chiều dài của lò xo là 15 cm:
\({x_1} = {l_1} - {l_0} = 15{\mkern 1mu} {\rm{cm}} - 10{\mkern 1mu} {\rm{cm}} = 5{\mkern 1mu} {\rm{cm}} = 0.05{\mkern 1mu} {\rm{m}}\)
- Độ giãn khi chiều dài của lò xo là 18 cm:
\({x_2} = {l_2} - {l_0} = 18{\mkern 1mu} {\rm{cm}} - 10{\mkern 1mu} {\rm{cm}} = 8{\mkern 1mu} {\rm{cm}} = 0.08{\mkern 1mu} {\rm{m}}\)
- Công của lực khi lò xo giãn từ \({x_1} = 0.05{\mkern 1mu} {\rm{m}}\) đến \({x_2} = 0.08{\mkern 1mu} {\rm{m}}\):
\(A = \int_{0.05}^{0.08} k x{\mkern 1mu} dx\)
Thay \(k = 800{\mkern 1mu} {\rm{N/m}}\) vào:
\(A = 800\int_{0.05}^{0.08} x {\mkern 1mu} dx\)
Tính tích phân:
\(A = 800\left[ {\frac{{{x^2}}}{2}} \right]_{0.05}^{0.08}\)
\(A = 800\left( {\frac{{{{0.08}^2}}}{2} - \frac{{{{0.05}^2}}}{2}} \right)\)
\(A = 800 \times \frac{{(0.0064 - 0.0025)}}{2}\)
\(A = 800 \times \frac{{0.0039}}{2} = 800 \times 0.00195 = 1.56{\mkern 1mu} {\rm{J}}\)
Vậy công của lực làm lò xo giãn từ 15 cm đến 18 cm là \(1.56{\mkern 1mu} {\rm{J}}\).