Giải mục 2 trang 17, 18, 19 SGK Toán 11 tập 2 - Cùng khám phá — Không quảng cáo

Câu 1

Một thí nghiệm cho thấy trong điều kiện môi trường sống lí tưởng và thức ăn dồi dào thì số lượng của một đàn chuột sẽ gấp đôi sau 55 ngày (nguồn: https://baotintuc.vn/ho-so/ky-la-thi-nghiem-xay-dung-xa-hoi-khong-tuong-cho-chuot-20181226104302132.htm ).

Giả sử lúc đầu, đàn chuột có 100 con. Như vậy, sau thời gian t ngày, số lượng chuột là $P = {100.2^{\frac{t}{{55}}}}$ con.

a) Mất bao lâu để đàn chuột đạt số lượng 2 000 con?

b) Tìm một hàm số t theo P để xác định thời gian t mà số lượng chuột đạt tới P (nếu có).

Phương pháp giải:

Thay P = 2000 vào $P = {100.2^{\frac{t}{{55}}}}$. Tìm t.

Lời giải chi tiết:

a) Ta có:

$\begin{array}{l}{100.2^{\frac{t}{{55}}}} = 2000\\ \Leftrightarrow {2^{\frac{t}{{55}}}} = 20\\ \Leftrightarrow \frac{t}{{55}} = {\log _2}20\\ \Leftrightarrow t = 55.{\log _2}20\\ \Leftrightarrow t \approx 237,71\end{array}$

b)

$\begin{array}{l}P = {100.2^{\frac{t}{{55}}}}\\ \Leftrightarrow \frac{P}{{100}} = {2^{\frac{t}{{55}}}}\\ \Leftrightarrow \frac{t}{{55}} = {\log _2}\frac{P}{{100}}\\ \Leftrightarrow t = 55.{\log _2}\frac{P}{{100}}\end{array}$

Vậy hàm số t theo P để xác định thời gian t mà số lượng chuột đạt tới P là: $t = 55.{\log _2}\frac{P}{{100}}$

Luyện tập 3

Tìm tập xác định của hàm số sau:

a) $y = \log \left( {2x - 3} \right)$

b) $y = 2 + {\log _{0,5}}\left( {{x^2} - 1} \right)$

c) $y = \ln \frac{{3x + 2}}{{1 - x}}$

Phương pháp giải:

Hàm số $y = {\log _a}\left( {u\left( x \right)} \right)\left( {a > 0,a \ne 1} \right)$ xác định khi $u\left( x \right) > 0$.

Lời giải chi tiết:

a) $y = \log \left( {2x - 3} \right)$ xác định khi $2x - 3 > 0 \Leftrightarrow x > \frac{3}{2}$

Vậy $D = \left( {\frac{3}{2}; + \infty } \right)$

b) $y = 2 + {\log _{0,5}}\left( {{x^2} - 1} \right)$ xác định khi ${x^2} - 1 > 0 \Leftrightarrow {x^2} > 1 \Leftrightarrow \left[ \begin{array}{l}x > 1\\x <  - 1\end{array} \right.$

Vậy $D = \mathbb{R}\backslash \left\{ 1 \right\}$

c) $y = \ln \frac{{3x + 2}}{{1 - x}}$ xác định khi  $\frac{{3x + 2}}{{1 - x}} > 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}3x + 2 > 0\\1 - x > 0\end{array} \right.\\\left\{ \begin{array}{l}3x + 2 < 0\\1 - x < 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x >  - \frac{2}{3}\\x < 1\end{array} \right.\\\left\{ \begin{array}{l}x <  - \frac{2}{3}\\x > 1\end{array} \right.\,{\rm{(L)}}\end{array} \right.$

Vậy $D = \left( {\frac{{ - 2}}{3};1} \right)$

Hoạt động 4

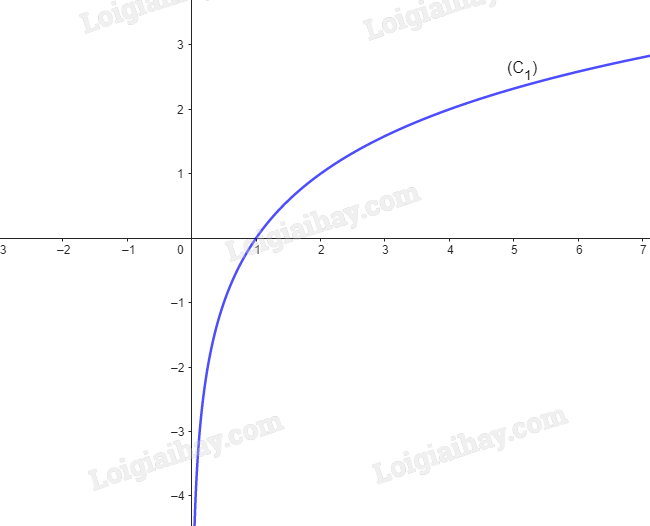
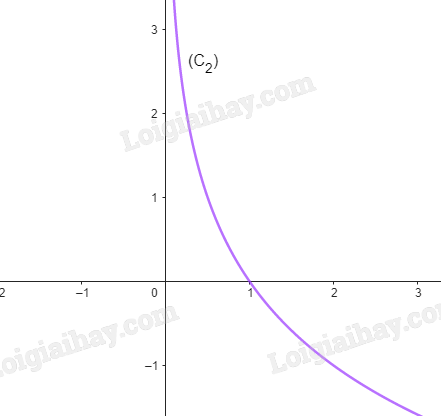
Cho hàm số $y = {\log _2}x$ có đồ thị là (C ₁ ) và hàm số $y = {\log _{0,5}}x$ có đồ thị (C ₂ ).

a) Hoàn thành bảng giá trị sau và biểu diễn trên hệ trục Oxy.

b) Vẽ đường cong nối các điểm thuộc (C ₁ ) (theo thứ tự hoành độ tăng dần) và một đường cong khác nối các điểm thuộc (C ₂ ) (theo thứ tự hoành độ tăng dần).

Phương pháp giải:

Thay lần lượt các giá trị của x vào hàm số.

Lời giải chi tiết:

a,

b,

Luyện tập 4

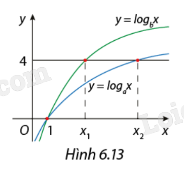
Hàm số $y = {\log _a}x$ và $y = {\log _b}x$ có đồ thị như Hình 6.13. Đường thẳng y = 4 cắt hai đồ thị tại các điểm có hoành độ x ₁ , x ₂ . Biết rằng x ₁ = 2x ₂ . Tính giá trị của $\frac{a}{b}$.

Phương pháp giải:

Thay y = 4 vào 2 hàm số. Áp dụng: ${\log _a}b = c \Leftrightarrow {a^c} = b$ để tính a, b lần lượt theo ${x_1},{x_2}$.

Lời giải chi tiết:

Ta có:

$\begin{array}{l}{\log _a}{x_1} = 4\\ \Leftrightarrow {a^4} = {x_1}\\ \Leftrightarrow {a^4} = 2{x_2}\\ \Leftrightarrow a = {\left( {2{x_2}} \right)^{\frac{1}{4}}}\end{array}$

$\begin{array}{l}{\log _b}{x_2} = 4\\ \Leftrightarrow {b^4} = {x_2}\\ \Leftrightarrow b = {\left( {{x_2}} \right)^{\frac{1}{4}}}\end{array}$

$\Rightarrow \frac{a}{b} = \frac{{{{\left( {2{x_2}} \right)}^{\frac{1}{4}}}}}{{{{\left( {{x_2}} \right)}^{\frac{1}{4}}}}} = {2^{\frac{1}{4}}}$