Giải mục 2 trang 35, 36 SGK Toán 11 tập 2 - Cùng khám phá
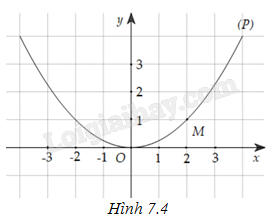
Cho hàm số \(f(x) = \frac{{{x^2}}}{4}\) có đồ thị là đường parabol (P) như Hình 7.4 . Gọi M là điểm thuộc (P) có hoành độ \({x_0} = 2\).
Hoạt động 3
Cho hàm số \(f(x) = \frac{{{x^2}}}{4}\) có đồ thị là đường parabol (P) như Hình 7.4 . Gọi M là điểm thuộc (P) có hoành độ \({x_0} = 2\).
a, Tính \({f'}(2)\)
b, Viết phương trình đường thẳng \(\Delta \) đi qua điểm M và có hệ số góc bằng \({f'}(2)\)
c, Vẽ đường thẳng \(\Delta \) và (P) trên cùng một mặt phẳng tọa độ. Có nhận xét gì về \(\Delta \) và (P).
Phương pháp giải:
a, Áp dụng định nghĩa tính \({f'}(2)\)
b, Phương trình đường thẳng đi qua điểm M có hoành độ \({x_0}\) và hệ số góc \({f'}(2)\) là
\(y = {f'}({x_0}).(x - {x_0})\)
c, Dựa vào câu b để vẽ đường thẳng \(\Delta \)
Lời giải chi tiết:
a, Ta có: \({f'}(2) = \mathop {\lim }\limits_{x \to 2} \frac{{f(x) - f(2)}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{\frac{{{x^2}}}{4} - 1}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 4}}{{4(x - 2)}} = \mathop {\lim }\limits_{x \to 2} \frac{{(x - 2).(x + 2)}}{{4(x - 2)}} = \mathop {\lim }\limits_{x \to 2} \frac{{x + 2}}{4} = 1\)
b, Điểm M có tọa độ M(2;1)
Phương trình đường thẳng \(\Delta \) đi qua điểm M(2,1) có hệ số góc \({f'}(2)\) là:
y = 1.( x-2)+1= x-1
Vậy phương trình đường thẳng \(\Delta \) là: y= x-1
Luyện tập 2
Cho hàm số \(y = - 3{x^3}\) có đồ thị ( C ). Tìm hệ số góc của tiếp tuyến tại điểm M (-1,3)
Phương pháp giải:
Hệ số góc của tiếp tuyến là đạo hàm của hàm số tại điểm -1
Lời giải chi tiết:
Ta có: \({f'}( - 1) = \mathop {\lim }\limits_{x \to - 1} \frac{{f(x) - f( - 1)}}{{x - ( - 1)}} = \mathop {\lim }\limits_{x \to - 1} \frac{{ - 3{x^3} - 3}}{{x + 1}} = \mathop {\lim }\limits_{x \to - 1} \frac{{ - 3.({x^3} + 1)}}{{x + 1}} = \mathop {\lim }\limits_{x \to - 1} ( - 3).({x^2} - x + 1) = - 9\)
Vậy hệ số góc của tiếp tuyến tại điểm M(-1,3) là -9.
Hoạt động 4
Cho hàm số \(f(x) = {x^2} + 1\)có đồ thị parabol (P) và điểm M(1,2) thuộc (P). Gọi \(\Delta \)là tiếp tuyến của (P) tại M. Hãy viết phương trình \(\Delta \).
Phương pháp giải:
Hệ số góc của tiếp tuyến là đạo hàm của hàm số tại điểm 1
Phương trình tiếp tuyến của đường thẳng có hệ số góc k tại điểm \(M({x_0};{y_0})\) là:
\(y = k.(x - {x_0}) + {y_0}\)
Lời giải chi tiết:
Ta có: \(y'(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(x) - f(1)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} + 1 - 2}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} (x + 1) = 2\)
Phương trình tiếp tuyến tại điểm M(1,2) có hệ số góc k=2 là:
y = 2.( x -1)+2=2x
Luyện tập 3
Cho parabol (P) \(y = {x^2} + 2x - 3\) và điểm M thuộc (P) có hoành độ \({x_0} = - 2\)
a, Tính \({y'}( - 2)\)
b, Viết phương trình tiếp tuyến của (P) tại điểm M.
Phương pháp giải:
a, Sử dụng định nghĩa để tìm đạo hàm của hàm số tại điểm -2
b, Sử dụng công thức tiếp tuyến \(y = {f'}({x_0}).(x - {x_0}) + f({x_0})\)
Lời giải chi tiết:
a, Ta có: \(y'( - 2) = \mathop {\lim }\limits_{x \to - 2} \frac{{f(x) - f( - 2)}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} \frac{{{x^2} + 2x - 3 - ( - 3)}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} \frac{{{x^2} + 2x}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} \frac{{x.(x + 2)}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} x = - 2\)
b, Ta có: \({x_0} = - 2 \Rightarrow f({x_0}) = {( - 2)^2} + 2.( - 2) - 3 = - 3\)
Phương trình tiếp tuyến của (P) tại điểm M (-2, -3) là:
y = -2. (x + 2) -3= -2x -7.