Giải mục 2 trang 32, 33, 34, 35, 36, 37, 38 SGK Toán 11 tập 1 - Cùng khám phá — Không quảng cáo

Hoạt động 2

Trong Hình 1.45, xét đường thẳng $y = m\left( { - 1 \le m \le 1} \right)$ và đồ thị hàm số $y = \sin x$.

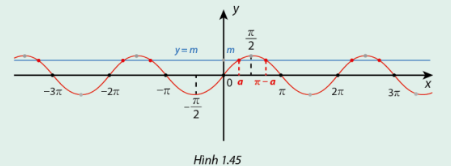
a) Dựa vào Hình 1.45, cho biết trên đoạn $\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]$, đồ thị hàm số $y = \sin x$ cắt đường thẳng $y = m$ tại điểm có hoành độ là giá trị nào.

b) Biểu diễn hoành độ của tất cả các giao điểm của đồ thị hàm số $y = \sin x$ và đường thẳng $y = m$ theo hoành độ của giao điểm trong câu a).

Phương pháp giải:

Quan sát hình vẽ để trả lời câu hỏi.

Lời giải chi tiết:

a) Dựa vào Hình 1.45, trên đoạn $\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]$, đồ thị hàm số $y = \sin x$ cắt đường thẳng $y = m$ tại điểm có hoành độ là $a$ và $\pi  - a$.

b) Hoành độ của tất cả các giao điểm lần lượt từ trái sang phải là $- 3\pi  - a;a - 2\pi ; - \pi  - a;a;\pi  - a;a + 2\pi ;3\pi  - a$.

Luyện tập 3

Giải các phương trình sau:

a) $\sin x = \frac{1}{3};$

b) $\sin 2x =  - \frac{1}{2};$

c) $\sin \left( {x + {{30}^0}} \right) = \frac{{\sqrt 2 }}{2}$.

Phương pháp giải:

$\begin{array}{l}\sin x = m \Leftrightarrow \sin x = \sin \alpha \\ \Rightarrow \left[ \begin{array}{l}x = \alpha  + k2\pi \\x = \pi  - \alpha  + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}$

Lời giải chi tiết:

a)

$\begin{array}{l}\sin x = \frac{1}{3}\\ \Leftrightarrow \sin x = \sin 0,34\\ \Rightarrow \left[ \begin{array}{l}x = 0,34 + k2\pi \\x = \pi  - 0,34 + k2\pi  \approx 2,8 + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy phương trình có các nghiệm là $x = 0,34 + k2\pi ,x = 2,8 + k2\pi \left( {k \in \mathbb{Z}} \right)$.

b)

$\begin{array}{l}\sin 2x =  - \frac{1}{2}\\ \Leftrightarrow \sin 2x = \sin \left( { - \frac{\pi }{6}} \right)\\ \Rightarrow \left[ \begin{array}{l}x =  - \frac{\pi }{6} + k2\pi \\x = \pi  - \left( { - \frac{\pi }{6}} \right) + k2\pi  = \frac{{7\pi }}{6} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy phương trình có các nghiệm là $x =  - \frac{\pi }{6} + k2\pi ,x = \frac{{7\pi }}{6} + k2\pi \left( {k \in \mathbb{Z}} \right)$.

c)

$\begin{array}{l}\sin \left( {x + {{30}^0}} \right) = \frac{{\sqrt 2 }}{2}\\ \Leftrightarrow \sin \left( {x + {{30}^0}} \right) = \sin \left( {{{45}^0}} \right)\\ \Rightarrow \left[ \begin{array}{l}x + {30^0} = {45^0} + k{360^0}\\x + {30^0} = {180^0} - {45^0} + k{360^0} = {135^0} + k{360^0}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x = {15^0} + k{360^0}\\x = {180^0} - {45^0} - {30^0} + k{360^0} = {105^0} + k{360^0}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy phương trình có các nghiệm là $x = {15^0} + k{360^0},x = {105^0} + k{360^0}\left( {k \in \mathbb{Z}} \right)$.

Luyện tập 4

Giải phương trình: $\sin 4x =  - \sin \left( {\pi  - x} \right)$.

Phương pháp giải:

$\begin{array}{l}\sin x =  - \sin \alpha \\ \Leftrightarrow \sin x = \sin \left( { - \alpha } \right)\\ \Rightarrow \left[ \begin{array}{l}x =  - \alpha  + k2\pi \\x = \pi  + \alpha  + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}$

Lời giải chi tiết:

$\begin{array}{l}\sin 4x =  - \sin \left( {\pi  - x} \right)\\ \Leftrightarrow \sin 4x = \sin \left( { - \pi  + x} \right)\\ \Rightarrow \left[ \begin{array}{l}4x =  - \pi  + x + k2\pi \\x = \pi  - \left( { - \pi  + x} \right) + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}3x =  - \pi  + k2\pi \\2x = 2\pi  + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x =  - \frac{\pi }{3} + k\frac{{2\pi }}{3}\\x = \pi  + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy phương trình có các nghiệm là $x =  - \frac{\pi }{3} + k\frac{{2\pi }}{3},x = \pi  + k\pi \left( {k \in \mathbb{Z}} \right)$.

Vận dụng 1

Giả sử số lượng N của một loài hươu sau t năm được xác định bởi công thức

$N = 30000 + 20000\sin \left( {\frac{{\pi t}}{{10}}} \right)$

Xác định năm đầu tiên mà số lượng của loài hươu này bằng 50 nghìn con theo công thức trên.

Phương pháp giải:

Thay N = 50000 vào phương trình. Giải phương trình lượng giác cơ bản để tìm t.

Lời giải chi tiết:

Thay N = 50000 vào phương trình, ta có:

$\begin{array}{l}30000 + 20000\sin \left( {\frac{{\pi t}}{{10}}} \right) = 50000\\ \Leftrightarrow \sin \left( {\frac{{\pi t}}{{10}}} \right) = 1\\ \Leftrightarrow \sin \left( {\frac{{\pi t}}{{10}}} \right) = \sin \left( {\frac{\pi }{2}} \right)\\ \Rightarrow \frac{{\pi t}}{{10}} = \frac{\pi }{2} + k2\pi \\ \Leftrightarrow t = 5 + k20\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy sau 5 năm đầu tiên thì số lượng của loài hươu này bằng 50 nghìn con.

Hoạt động 3

Trong Hình 1.46, xét đường thẳng $y = m\left( { - 1 \le m \le 1} \right)$ và đồ thị hàm số $y = \cos x$.

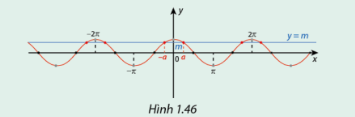
a) Dựa vào Hình 1.46, cho biết trên đoạn $\left[ {0;\pi } \right]$, đồ thị hàm số $\cos x = m$ cắt đường thẳng $y = m$ tại điểm có hoành độ là giá trị nào.

b) Biểu diễn hoành độ của tất cả các giao điểm của đồ thị hàm số $y = \cos x$ và đường thẳng $y = m$ theo hoành độ của giao điểm trong câu a).

Phương pháp giải:

Quan sát hình vẽ để trả lời câu hỏi.

Lời giải chi tiết:

a) Dựa vào Hình 1.46, trên đoạn $\left[ {0;\pi } \right]$, đồ thị hàm số $\cos x = m$ cắt đường thẳng $y = m$ tại điểm có hoành độ là $- a$ và $a$.

b) Hoành độ của tất cả các giao điểm của đồ thị hàm số $y = \cos x$ và đường thẳng $y = m$ lần lượt từ trái sang phải là $- a - 2\pi ;a - 2\pi ; - a;a; - a + 2\pi ;a + 2\pi$.

Luyện tập 5

Giải các phương trình sau:

a) $\cos 2x = \cos \frac{\pi }{3};$

b) $\cos \left( {x + \frac{\pi }{4}} \right) =  - 1;$

c) $\cos \left( {x - {{45}^0}} \right) = \frac{{\sqrt 3 }}{2}.$

Phương pháp giải:

$\begin{array}{l}\cos x = m\\ \Leftrightarrow \cos x = \cos \alpha \\ \Rightarrow \left[ \begin{array}{l}x = \alpha  + k2\pi \\x =  - \alpha  + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}$

Lời giải chi tiết:

a)

$\begin{array}{l}\cos 2x = \cos \frac{\pi }{3}\\ \Rightarrow \left[ \begin{array}{l}2x = \frac{\pi }{3} + k2\pi \\2x =  - \frac{\pi }{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k\pi \\x =  - \frac{\pi }{6} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy phương trình có các nghiệm là $x = \frac{\pi }{6} + k\pi ,x =  - \frac{\pi }{6} + k\pi \left( {k \in \mathbb{Z}} \right)$

b)

$\begin{array}{l}\cos \left( {x + \frac{\pi }{4}} \right) =  - 1\\ \Leftrightarrow x + \frac{\pi }{4} = \pi  + k2\pi \left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow x = \frac{{3\pi }}{4} + k2\pi \left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy phương trình có các nghiệm là $x = \frac{{3\pi }}{4} + k2\pi \left( {k \in \mathbb{Z}} \right)$

c)

$\begin{array}{l}\cos \left( {x - {{45}^0}} \right) = \frac{{\sqrt 3 }}{2}\\ \Leftrightarrow \cos \left( {x - {{45}^0}} \right) = \cos \left( {{{30}^0}} \right)\\ \Rightarrow \left[ \begin{array}{l}x - {45^0} = {30^0} + k{360^0}\\x - {45^0} =  - {30^0} + k{360^0}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x = {75^0} + k{360^0}\\x = {15^0} + k{360^0}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy phương trình có các nghiệm là $x = {75^0} + k{360^0},x = {15^0} + k{360^0}\left( {k \in \mathbb{Z}} \right)$

Luyện tập 6

Giải phương trình sau: $\sin 5x =  - \cos \left( {\pi  + x} \right).$

Phương pháp giải:

Đưa phương trình về dạng $\cos x = \cos \alpha$$\Rightarrow \left[ \begin{array}{l}x = \alpha  + k2\pi \\x =  - \alpha  + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)$

Lời giải chi tiết:

$\begin{array}{l}\sin 5x =  - \cos \left( {\pi  + x} \right)\\ \Leftrightarrow \cos \left( {\frac{\pi }{2} - 5x} \right) = \cos \left( {\pi  + x} \right)\\ \Rightarrow \left[ \begin{array}{l}\frac{\pi }{2} - 5x = \pi  + x + k2\pi \\\frac{\pi }{2} - 5x =  - \pi  - x + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l} - 6x = \frac{\pi }{2} + k2\pi \\ - 4x =  - \frac{{3\pi }}{2} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x =  - \frac{\pi }{{12}} - k\frac{\pi }{3}\\x = \frac{{3\pi }}{8} - k\frac{\pi }{2}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy phương trình có các nghiệm là $x =  - \frac{\pi }{{12}} - k\frac{\pi }{3},x = \frac{{3\pi }}{8} - k\frac{\pi }{2}$

Vận dụng 2

Cường độ dòng điện i (ampe) qua một mạch điện xoay chiều được tính bởi công thức $i = 10\sqrt 2 \cos \left( {100\pi t} \right),$ trong đó t là thời gian tính bằng giây. Xác định thời điểm đầu tiên cường độ dòng điện bằng 10 ampe.

Phương pháp giải:

Thay i = 10 vào công thức. Giải phương trình lượng giác cơ bản để tìm t.

Lời giải chi tiết:

Thay i = 10 vào công thức, ta có:

$\begin{array}{l}10\sqrt 2 \cos \left( {100\pi t} \right) = 10\\ \Leftrightarrow \cos \left( {100\pi t} \right) = \frac{1}{{\sqrt 2 }}\\ \Leftrightarrow \cos \left( {100\pi t} \right) = \cos \left( {\frac{\pi }{4}} \right)\\ \Rightarrow \left[ \begin{array}{l}100\pi t = \frac{\pi }{4} + k2\pi \\100\pi t =  - \frac{\pi }{4} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}t = \frac{1}{{400}} + \frac{k}{{50}}\\t =  - \frac{1}{{400}} + \frac{k}{{50}}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy thời điểm đầu tiên cường độ dòng điện bằng 10 ampe là $\frac{1}{{400}}$ giây.

Hoạt động 4

Trong Hình 1.47, xét đường thẳng $y = m$ và đồ thị hàm số $y = \tan x$.

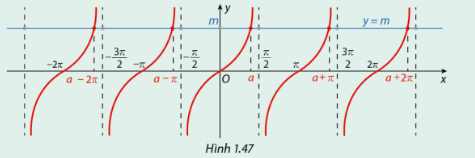
a) Dựa vào Hình 1.47, cho biết trên đoạn $\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)$, đồ thị hàm số $y = \tan x$ cắt đường thẳng $y = m$ tại điểm có hoành độ là giá trị nào.

b) Biểu diễn hoành độ của tất cả các giao điểm của đồ thị hàm số $y = \tan x$ và đường thẳng $y = m$ theo hoành độ của giao điểm trong câu a).

Phương pháp giải:

Quan sát hình vẽ để trả lời.

Lời giải chi tiết:

a) Dựa vào Hình 1.47, trên đoạn $\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)$, đồ thị hàm số $y = \tan x$ cắt đường thẳng $y = m$ tại điểm có hoành độ là $a$.

b) Hoành độ của tất cả các giao điểm của đồ thị hàm số $y = \tan x$ và đường thẳng $y = m$ lần lượt từ trái sang phải là $a - 2\pi ,a - \pi ,a,a + \pi ,a + 2\pi$.

Luyện tập 7

Giải các phương trình sau:

a) $\tan 3x = 1;$

b) $\tan 4x =  - 1,5;$

c) $\tan \left( {x + {{15}^0}} \right) =  - \sqrt 3 .$

Phương pháp giải:

$\begin{array}{l}\tan x = m\\ \Leftrightarrow \tan x = \tan \alpha \\ \Leftrightarrow x = \alpha  + k\pi \left( {k \in \mathbb{Z}} \right)\end{array}$

Lời giải chi tiết:

a)

$\begin{array}{l}\tan 3x = 1\\ \Leftrightarrow \tan 3x = \tan \frac{\pi }{4}\\ \Leftrightarrow 3x = \frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow x = \frac{\pi }{{12}} + k\frac{\pi }{3}\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy phương trình có nghiệm là $x = \frac{\pi }{{12}} + k\frac{\pi }{3}\left( {k \in \mathbb{Z}} \right)$

b) Gọi a là góc lượng giác thuộc khoảng $\left( {0;\pi } \right)$ thỏa mãn $\tan 4x =  - 1,5$

$\begin{array}{l}\tan 4x = \tan a\\ \Leftrightarrow 4x = a + k\pi \left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow x = \frac{a}{4} + k\frac{\pi }{4}\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy phương trình có nghiệm là $x = \frac{a}{4} + k\frac{\pi }{4}\left( {k \in \mathbb{Z}} \right)$

c)

$\begin{array}{l}\tan \left( {x + {{15}^0}} \right) =  - \sqrt 3 \\ \Leftrightarrow \tan \left( {x + {{15}^0}} \right) = \tan \left( { - {{60}^0}} \right)\\ \Leftrightarrow x + {15^0} =  - {60^0} + k{180^0}\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow x =  - {75^0} + k{180^0}\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy phương trình có nghiệm là $x =  - {75^0} + k{180^0}\left( {k \in \mathbb{Z}} \right)$

Vận dụng 3

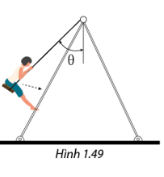
Một người dẫn em gái của mình đến công viên để chơi xích đu. Lực đẩy theo phương ngang F (N) mà người đó dùng để đẩy em gái trong trò chơi này được xác định bởi công thức $F = mg\tan \theta$, trong đó m (kg) là khối lượng của em gái, g là gia tốc trọng trường và $\theta$ là góc tạo bởi xích đu khi bắt đầu được đẩy với phương thẳng đứng (Hình 1.49) (nguồn: https://www.khanacademy.org/science/physics/centripetal-force-and-gravitation/centripetal-forces/v/mass-swiging-in-a-horizontal-circle ). Xác định góc $\theta$ khi $F = 400\sqrt 3$N, m = 40 kg và g = 10 m/s ² .

Phương pháp giải:

Thay $F = 400\sqrt 3$, m = 40 và g = 10 vào công thức. Giải phương trình lượng giác cơ bản để tìm $\theta$.

Lời giải chi tiết:

$\begin{array}{l}400\sqrt 3  = 40.10.\tan \theta \\ \Leftrightarrow \tan \theta  = \sqrt 3 \\ \Leftrightarrow \tan \theta  = \tan {60^0}\\ \Leftrightarrow \theta  = {60^0} + k{180^0}\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy $\theta  = {60^0}$

Hoạt động 5

Trong Hình 1.50, xét đường thẳng $y = m$và đồ thị hàm số $y = \cot x$.

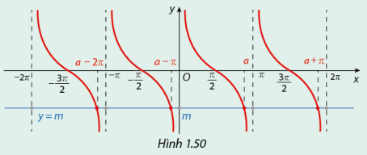
a) Dựa vào Hình 1.50, cho biết trên đoạn $\left( {0;\pi } \right)$, đồ thị hàm số $y = \cot x$ cắt đường thẳng $y = m$ tại điểm có hoành độ là giá trị nào.

b) Biểu diễn hoành độ của tất cả các giao điểm của đồ thị hàm số $y = \cot x$ và đường thẳng $y = m$ theo hoành độ của giao điểm trong câu a).

Phương pháp giải:

Quan sát hình vẽ để trả lời.

Lời giải chi tiết:

a) Dựa vào Hình 1.50, trên đoạn $\left( {0;\pi } \right)$, đồ thị hàm số $y = \cot x$ cắt đường thẳng $y = m$ tại điểm có hoành độ là $a$.

b) Hoành độ của tất cả các giao điểm của đồ thị hàm số $y = \cot x$ và đường thẳng $y = m$ lần lượt từ trái sang phải là $a - 2\pi ,a - \pi ,a,a + \pi$.

Luyện tập 8

Giải các phương trình sau:

a) $\cot 2x =  - 1;$

b) $\cot 6x = 4;$

c) $\cot \left( {x - {{45}^0}} \right) = \sqrt 3 .$

Phương pháp giải:

$\begin{array}{l}\cot a = m \Leftrightarrow \cot a = \cot b\\ \Leftrightarrow a = b + k\pi \left( {k \in \mathbb{Z}} \right)\end{array}$

Lời giải chi tiết:

a)

$\begin{array}{l}\cot 2x =  - 1\\ \Leftrightarrow \cot 2x = \cot \left( { - \frac{\pi }{4}} \right)\\ \Leftrightarrow 2x =  - \frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow x =  - \frac{\pi }{8} + k\frac{\pi }{2}\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy phương trình có nghiệm là $x =  - \frac{\pi }{8} + k\frac{\pi }{2}\left( {k \in \mathbb{Z}} \right)$

b) Gọi a là góc lượng giác thuộc khoảng $\left( {0;\pi } \right)$ thỏa mãn $\cot 6x = 4$

$\begin{array}{l}\cot 6x = \cot a\\ \Leftrightarrow 6x = a + k\pi \left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow x = \frac{a}{6} + k\frac{\pi }{6}\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy phương trình có nghiệm là $x = \frac{a}{6} + k\frac{\pi }{6}\left( {k \in \mathbb{Z}} \right)$

c)

$\begin{array}{l}\cot \left( {x - {{45}^0}} \right) = \sqrt 3 \\ \Leftrightarrow \cot \left( {x - {{45}^0}} \right) = \cot \left( {{{30}^0}} \right)\\ \Leftrightarrow x - {45^0} = {30^0} + k{180^0}\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow x = {75^0} + k{180^0}\left( {k \in \mathbb{Z}} \right)\end{array}$

Vậy phương trình có nghiệm là $x = {75^0} + k{180^0}\left( {k \in \mathbb{Z}} \right)$