Giải mục 2 trang 22, 23 SGK Toán 11 tập 2 - Cùng khám phá — Không quảng cáo

Hoạt động 2

Ta biết: Với (C ₁ ) là đồ thị của hàm số y = f(x) và (C ₂ ) là đồ thị của hàm số y = g(x) thì tập hợp giá trị của x để (C ₁ ) nằm phía trên (C ₂ ) là tập nghiệm của bất phương trình f(x) > g(x).

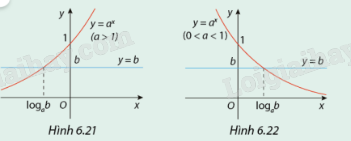
Quan sát các đồ thị (Hình 6.21 và 6.22) trong Hoạt động 1 và trong mỗi trường hợp, hãy tìm các tập nghiệm của bất phương trình a ^x > b:

a) Khi b > 0;

b) Khi b ≤ 0.

Phương pháp giải:

Quan sát hình vẽ.

Lời giải chi tiết:

a) Khi b > 0:

a > 1: a ^x > b $\Leftrightarrow x > {\log _a}b$

0 < a < 1: a ^x > b $\Leftrightarrow x < {\log _a}b$

b) Khi b ≤ 0 thì bất phương trình nghiệm đúng với mọi $x \in \mathbb{R}$.

Luyện tập 2

Giải các bất phương trình sau:

a) ${2^{x + 1}} > {2^{3x + 5}}$

b) ${\left( {\frac{7}{9}} \right)^{2{x^2} - 3x}} \le \frac{9}{7}$

Phương pháp giải:

Khi a > 1: ${a^{A\left( x \right)}} > {a^{B\left( x \right)}} \Leftrightarrow A\left( x \right) > B\left( x \right)$

Khi 0 < a < 1: ${a^{A\left( x \right)}} > {a^{B\left( x \right)}} \Leftrightarrow A\left( x \right) < B\left( x \right)$

Lời giải chi tiết:

a)

$\begin{array}{l}{2^{x + 1}} > {2^{3x + 5}}\\ \Leftrightarrow x + 1 > 3x + 5\\ \Leftrightarrow  - 2x > 4\\ \Leftrightarrow x <  - 2\end{array}$

Vậy tập nghiệm của bất phương trình đã cho là $\left( { - \infty ; - 2} \right)$.

b)

$\begin{array}{l}{\left( {\frac{7}{9}} \right)^{2{x^2} - 3x}} \le \frac{9}{7}\\ \Leftrightarrow {\left( {\frac{7}{9}} \right)^{2{x^2} - 3x}} \le {\left( {\frac{7}{9}} \right)^{ - 1}}\\ \Leftrightarrow 2{x^2} - 3x \ge  - 1\\ \Leftrightarrow 2{x^2} - 3x + 1 \ge 0\\ \Leftrightarrow \left[ \begin{array}{l}x \ge 1\\x \le \frac{1}{2}\end{array} \right.\end{array}$

Vậy tập nghiệm của bất phương trình đã cho là $\left( { - \infty ;\frac{1}{2}} \right) \cup \left( {1; + \infty } \right)$.