Giải mục 2 trang 58 Chuyên đề học tập Toán 10 - Cánh diều
Trong mặt phẳng tọa độ \(Oxy\), ta xét parabol (P) với phương trình chính tắc \({y^2} = 2px\) trong đó \(p > 0\) (Hình 20)
HĐ 2
Trong mặt phẳng tọa độ \(Oxy\), ta xét parabol (P) với phương trình chính tắc \({y^2} = 2px\) trong đó \(p > 0\) (Hình 20)
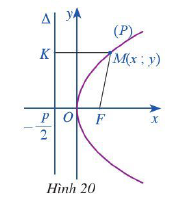
a) So sánh khoảng cách từ MF từ điểm M đến tiêu điểm F và khoảng cách MK từ điểm M đến đường thẳng \(\Delta \)
b) Tính độ dài đoạn thẳng MK. Từ đó tính độ dài đoạn thẳng MF
Phương pháp giải:
Cho parabol có PTCT: \({y^2} = 2px\) trong đó \(p > 0\)
+ Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)
+ Đường chuẩn: \(\Delta :x = - \frac{p}{2}\)
Lời giải chi tiết:
a) Khoảng cách MF từ điểm M đến tiêu điểm F bằng khoảng cách MK từ điểm M đến đường chuẩn \(\Delta \)
b) Ta có
\(MF = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \sqrt {{x^2} - px + \frac{{{p^2}}}{4} + 2px} = \sqrt {{x^2} + px + \frac{{{p^2}}}{4}} = \sqrt {{{\left( {x + \frac{p}{2}} \right)}^2}} = x + \frac{p}{2}\)
Phương trình đường chuẩn \(\Delta :x = - \frac{p}{2} \Rightarrow \Delta :x + 0y + \frac{p}{2} = 0\)
Khoảng cách MK từ điểm M đến đường thẳng \(\Delta \) là: \(MK = \frac{{\left| {x + 0y + \frac{p}{2}} \right|}}{{\sqrt {{1^2} + {0^2}} }} = \left| {x + \frac{p}{2}} \right| = x + \frac{p}{2}\)
Vậy \(MF = MK = x + \frac{p}{2}\)
Luyện tập
a) Lập phương trình chính tắc của parabol (P), biết phương trình đường chuẩn là \(x = - 2\)
b) Tìm tọa độ tiêu điểm của parabol (P)
c) Tìm tọa độ điểm M thuộc parabol (P), biết khoảng cách từ M đến tiêu điểm bằng 6
Phương pháp giải:
Cho parabol có PTCT: \({y^2} = 2px\) trong đó \(p > 0\)
+ Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)
+ Đường chuẩn: \(\Delta :x = - \frac{p}{2}\)
Lời giải chi tiết:
a) Ta có phương trình đường chuẩn \(x = - 2 \Rightarrow \frac{p}{2} = 2 \Rightarrow p = 4\)
Vậy phương trình chính tắc của parabol (P) là \({y^2} = 8x\)
b) Tiêu điểm của parabol (P) là \(F\left( {2;0} \right)\)
c) Khoảng cách từ M đến tiêu điểm \(F\left( {2;0} \right)\) bằng 6 nên \(x + \frac{p}{2} = 6 \Rightarrow x + 2 = 6 \Rightarrow x = 4 \Rightarrow {y^2} = 8.4 \Rightarrow y = \pm 4\sqrt 2 \)
Vậy \(M\left( {4; \pm 4\sqrt 2 } \right)\)