Lý thuyết Định lí Viète và ứng dụng Toán 9 Kết nối tri thức
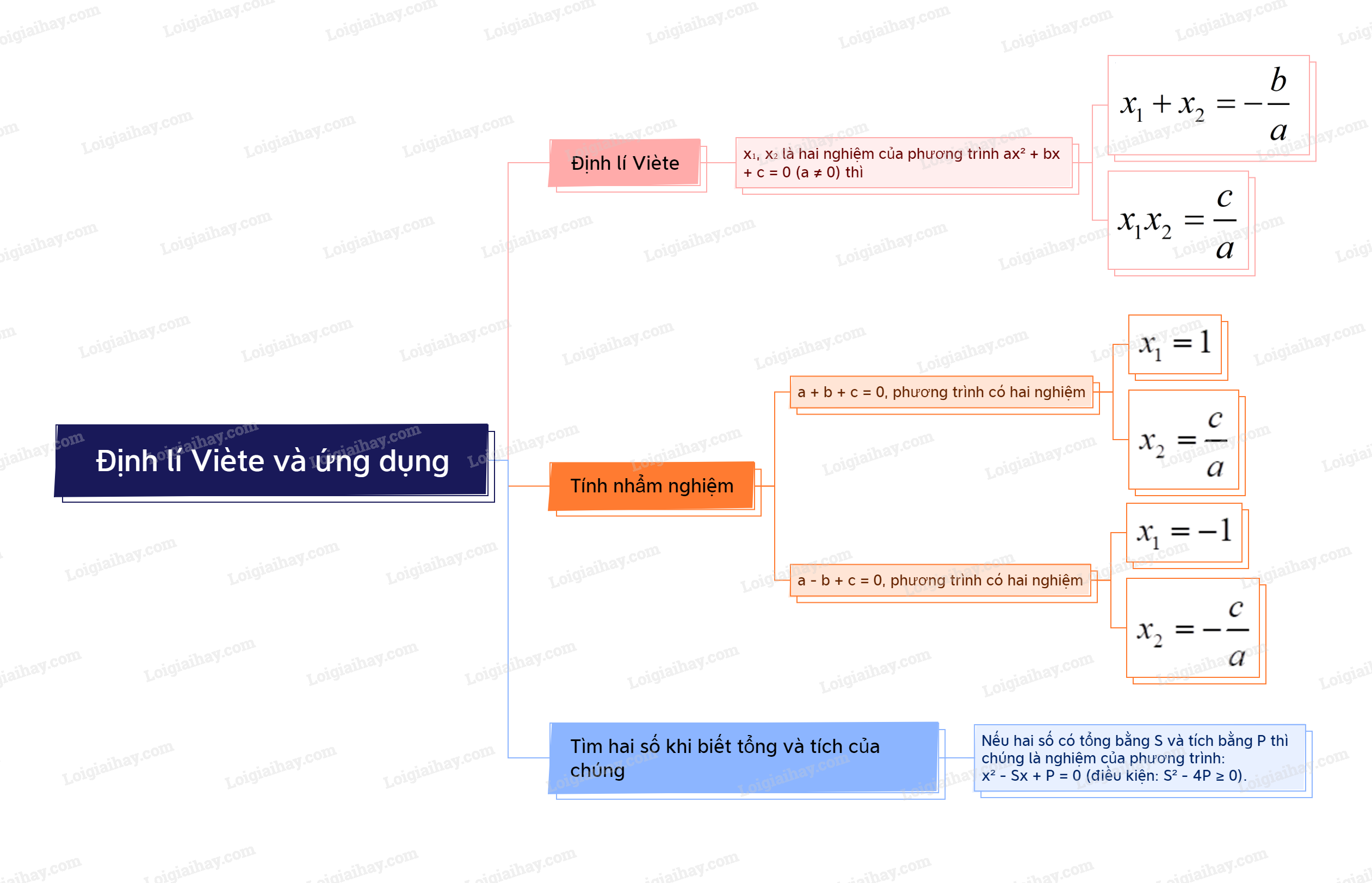
1. Định lí Viète Nếu \({x_1},{x_2}\) là hai nghiệm của phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) thì \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{a}\\{x_1}{x_2} = \frac{c}{a}.\end{array} \right.\)
1. Định lí Viète
|
Nếu \({x_1},{x_2}\) là hai nghiệm của phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) thì \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{a}\\{x_1}{x_2} = \frac{c}{a}.\end{array} \right.\) |
Ví dụ: Phương trình \(2{x^2} + 11x + 7 = 0\) có: \(\Delta = {11^2} - 4.2.7 = 65 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1},{x_2}\).
Theo định lí Viète, ta có: \({x_1} + {x_2} = - \frac{{11}}{2};{x_1}{x_2} = \frac{7}{2}\).
2. Áp dụng định lí Viète để tính nhẩm nghiệm
Giải phương trình bậc hai khi biết một nghiệm của nó
|
Xét phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\). - Nếu \(a + b + c = 0\) thì phương trình có một nghiệm là \({x_1} = 1\), còn nghiệm kia là \({x_2} = \frac{c}{a}\). - Nếu \(a - b + c = 0\) thì phương trình có nghiệm là \({x_1} = - 1\), còn nghiệm kia là \({x_2} = - \frac{c}{a}\). |
Ví dụ: Phương trình \({x^2} - 6x + 5 = 0\) có \(a + b + c = 1 + \left( { - 6} \right) + 5 = 0\) nên phương trình có hai nghiệm: \({x_1} = 1,{x_2} = 5\).
Phương trình \(5{x^2} + 14x + 9 = 0\) có \(a - b + c = 5 - 14 + 9 = 0\) nên phương trình có hai nghiệm: \({x_1} = - 1,{x_2} = - \frac{9}{5}\).
3 . Tìm hai số khi biết tổng và tích của chúng
|
Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là hai nghiệm của phương trình bậc hai: \({x^2} - Sx + P = 0\). Điều kiện để có hai số đó là \({S^2} - 4P \ge 0\). |
Ví dụ: Hai số có tổng bằng 9, tích bằng 20 là nghiệm của phương trình \({x^2} + 9x + 20 = 0\).
Ta có: \(\Delta = {\left( { - 9} \right)^2} - 4.1.20 = 1,\sqrt \Delta = 1\).
Suy ra phương trình có hai nghiệm \({x_1} = \frac{{9 - 1}}{2} = 4;{x_2} = \frac{{9 + 1}}{2} = 5\).
Vậy hai số cần tìm là 4 và 5.