Lý thuyết Vị trí tương đối của hai đường tròn Toán 9 Kết nối tri thức
1. Hai đường tròn cắt nhau
1. Hai đường tròn cắt nhau
|
Nếu hai đường tròn có đúng một điểm chung thì ta gọi đó là hai đường tròn cắt nhau . Hai điểm chung đó là hai giao điểm của chúng. |
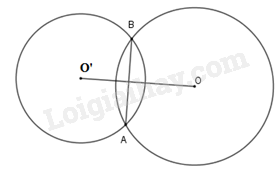
Hai đường tròn (O;R) và (O;R’) cắt nhau khi
\(R - R' < OO' < R + R'\) (với \(R > R'\))
Ví dụ: Cho OO’ = 5cm, khi đó hai đường tròn (O;4cm) và (O’;3cm) cắt nhau vì:
4cm – 3cm = 1cm < 5cm < 7cm = 4cm + 3cm.
2. Hai đường tròn tiếp xúc với nhau
|
Nếu hai đường tròn có duy nhất một điểm chung thì ta nói đó là hai đường tròn tiếp xúc với nhau . Điểm chung đó gọi là tiếp điểm của chúng. |
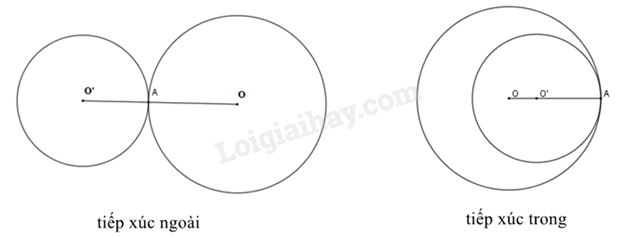
+ Hai đường tròn (O;R) và (O’;R’) tiếp xúc ngoài khi \(OO' = R + R'\).
+ Hai đường tròn (O;R) và (O’;R’) tiếp xúc trong khi \(OO' = R - R'\left( {R > R'} \right)\).
Nếu hai đường tròn tiếp xúc với nhau thì tiếp điểm thẳng hàng với hai tâm.
Ví dụ:
Cho OO’ = 5cm, khi đó hai đường tròn (O;3cm) và (O’;2cm) tiếp xúc ngoài với nhau vì 5cm = 3cm + 2cm.
Cho OO’ = 3cm, khi đó hai đường tròn (O;8cm) và (O’;5cm) tiếp xúc trong với nhau vì 3cm = 8cm - 5cm.
3. Hai đường tròn không giao nhau
|
Nếu hai đường tròn không có điểm chung nào thi ta nói đó là hai đường tròn không giao nhau. |
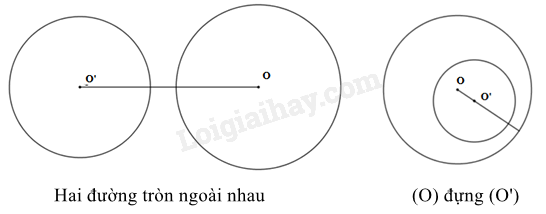
- Hai đường tròn (O;R) và (O’;R’) ngoài nhau khi \(OO' > R + R'\);
- Đường tròn (O;R) đựng đường tròn (O’;R’) khi \(R > R'\) và \(OO' < R - R'\).
Khi O trùng với O’ và \(R \ne R'\) thì ta có hai đường tròn đồng tâm.
Ví dụ: Cho đường tròn (O;3cm) và (O’;4cm) có \(OO' > 8cm\) thì \(OO' = 8cm > 3cm + 4cm = R + R'\) nên (O;3cm) và (O’;4cm) là hai đường tròn ngoài nhau.
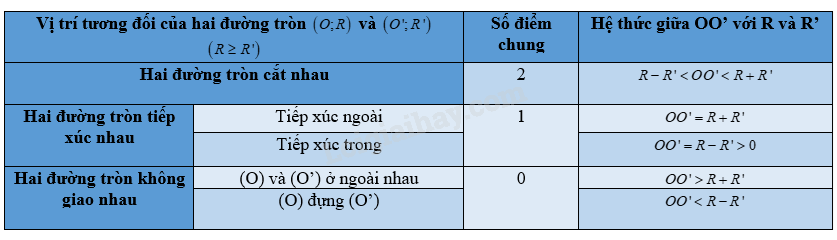
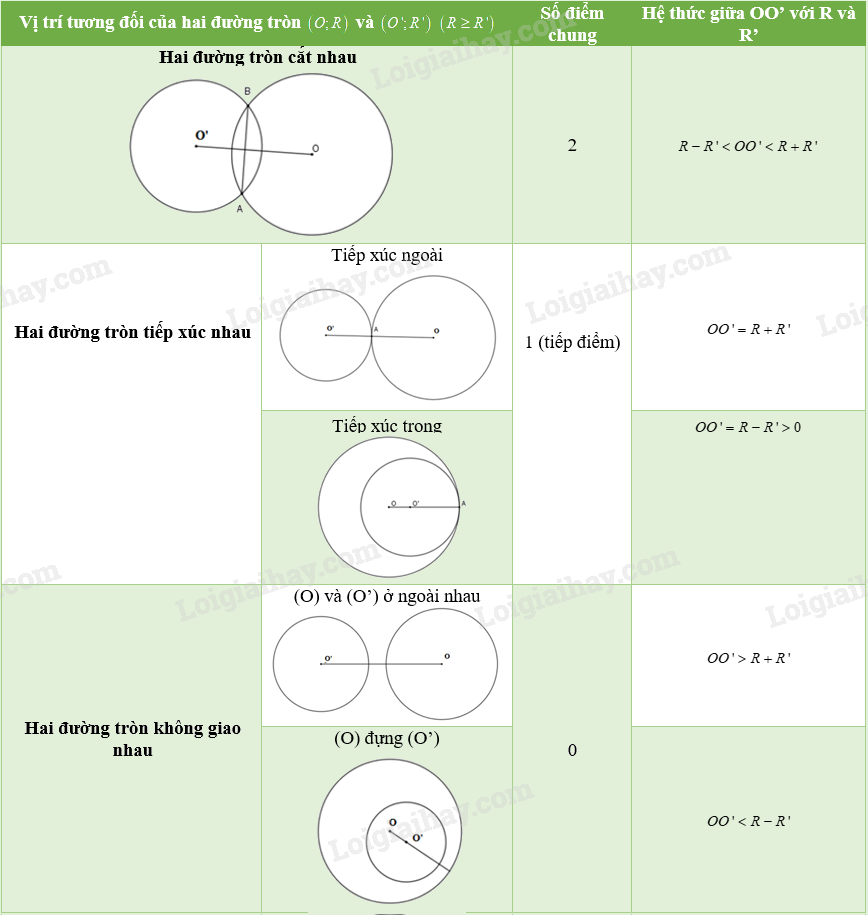
Bảng tổng kết vị trí tương đối của hai đường tròn