Lý thuyết Đa giác đều Toán 9 Kết nối tri thức
1. Đa giác đều Đa giác Những hình như dưới đây được gọi chung là các đa giác.
1. Đa giác đều
Đa giác
Những hình như dưới đây được gọi chung là các đa giác.
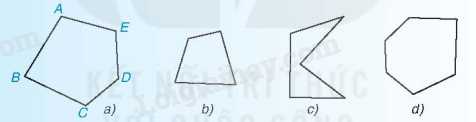
- Đa giác ABCDE (hình a) là hình gồm năm đoạn thẳng AB, BC, CD, DE, EA, trong đó bất kì hai đoạn thẳng nào có một điểm chung cũng không cùng nằm trên một đường thẳng.
Đa giác ABCDE có:
+ năm đỉnh là các điểm A, B, C, D, E,
+ năm cạnh là các đoạn thẳng AB, BC, CD, DE, EA
+ năm góc là các góc EAB, ABC, BCD, CDE, DEA.
- Nếu với một cạnh bất kì, các đỉnh không thuộc cạnh đó đều nằm về một phía đối với đường thẳng chứa cạnh đó thì đa giác được gọi là đa giác lồi. Các đa giác trong a, b, d là các đa giác lồi. Đa giác trong c không phải đa giác lồi.
Đa giác đều
|
Đa giác đều là một đa giác lồi có các cạnh bằng nhau và các góc bằng nhau. |
Các đỉnh của mỗi đa giác đều luôn cùng nằm trên một đường tròn, được gọi là đường tròn ngoại tiếp đa giác, tâm đường tròn được gọi là tâm của đa giác và đa giác được gọi là nội tiếp đường tròn đó.
Ví dụ: Một số hình đa giác đều thường gặp trong hình học:

2. Phép quay
Khái niệm phép quay
|
Phép quay thuận chiều \(\alpha ^\circ \) (0° < \(\alpha ^\circ \) < 360°) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \(\alpha ^\circ \) (hình a). Định nghĩa tương tự cho phép quay ngược chiều \(\alpha ^\circ \) tâm O (hình b). Chú ý: Phép quay 0° và phép quay 360° giữ nguyên mọi điểm.
|
Phép quay giữ nguyên hình đa giác đều
|
Một phép quay được gọi là giữ nguyên một đa giác đều ℋ nếu phép quay đó biến mỗi điểm của ℋ thành một điểm của ℋ . Nếu một phép quay biến các đỉnh của đa giác đều ℋ thành các đỉnh của ℋ thì phép quay đó giữ nguyên ℋ . |
Ví dụ:
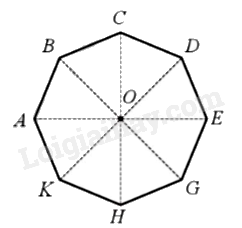
Phép quay thuận chiều \(45^\circ \) tâm O biến điểm A thành điểm B thì phép quay đó biến các điểm C, D, H, K tương ứng thành các điểm D, E, K, A.