Nửa đường tròn đơn vị - Giá trị lượng giác của một góc - Cách xác định điểm trên nửa đường tròn đơn vị tương ứng với góc - Cách xác định góc tương ứng với điểm trên nửa đường tròn đơn vị — Không quảng cáo

1. Lý thuyết

+) Nửa đường tròn đơn vị : nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành.

+) Với mỗi góc $\alpha ({0^o} \le \alpha  \le {180^o})$có duy nhất điểm $M({x_0};{y_0})$ trên nửa đường tròn đơn vị để $\widehat {xOM} = \alpha .$ Khi đó:

$\sin \alpha  = {y_0}$ là tung độ của M

$\cos \alpha  = {x_0}$ là hoành độ của M

$\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}}(\alpha  \ne {90^o})$

$\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}(\alpha  \ne {0^o},\alpha  \ne {180^o})$

+ Nhận xét:

${0^ \circ } < \alpha  < {90^ \circ }:\cos \alpha  > 0,\sin \alpha  > 0,\tan \alpha  > 0,\cot \alpha  > 0.$

${90^ \circ } < \alpha  < {180^ \circ }:\cos \alpha  < 0,\sin \alpha  > 0,\tan \alpha  < 0,\cot \alpha  < 0.$

+ Cách xác định điểm trên nửa đường tròn đơn vị tương ứng với góc $\alpha$

Bước 1. Ta đã biết góc $\alpha$, sử dụng máy tính hoặc các công cụ khác để tìm $\sin \alpha$ và $\cos \alpha$.

Bước 2. Xác định M trên hệ trục, với ${x_M} = \cos \alpha$ và ${y_M} = \sin \alpha$

+ Cách xác định góc tương ứng với điểm trên nửa đường tròn đơn vị.

Ta đã biết điểm M, tức là đã biết hoành độ và tung độ của M, kí hiệu là ${x_M},{y_M}.$

Bước 1. Đặt $\alpha  = \widehat {xOM}$, là góc cần tìm. Khi đó ${x_M} = \cos \alpha$ và ${y_M} = \sin \alpha$

Bước 2. Sử dụng máy tính hoặc các công cụ khác để tìm $\alpha$.

2. Ví dụ minh họa

Ví dụ 1. Tìm các giá trị lượng giác của góc ${63^o}$

Sử dụng máy tính cầm tay, ta được:

$\begin{array}{l}\sin {63^o} \approx 0,891\\\cos {63^o} \approx 0,454\\\tan {63^o} \approx 1,963\\\cot {63^o} = 1:\tan {63^o} \approx 0,51\end{array}$

Ví dụ 2. Tìm góc $\alpha ({0^o} \le \alpha  \le {180^o})$ thỏa mãn $\sin \alpha  = 0,67$

Trên nửa đường tròn đơn vị, lấy điểm M sao cho ${y_M} = 0,67$. Dễ thấy có 2 điểm thỏa mãn, gọi là M và M’.

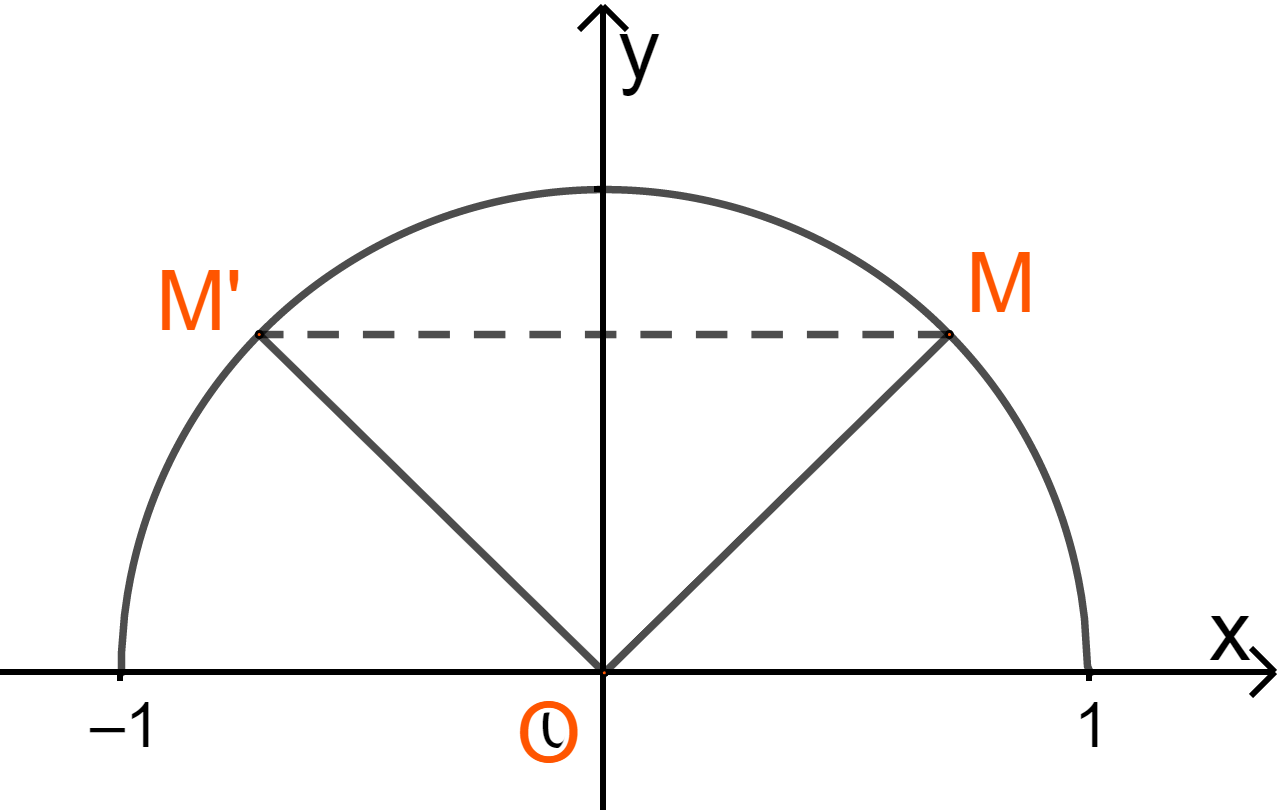
Do đó có hai góc thỏa mãn là $\widehat {xOM}$ và $\widehat {xOM'}$, trong đó $\widehat {xOM} < {90^ \circ } < \widehat {xOM'}$.

Vì M và M’ đối xứng nhau qua Oy nên $\widehat {MOy} = \widehat {M'Oy}$$\Rightarrow \widehat {M'Oy} = {90^ \circ } - \widehat {xOM} \Rightarrow \widehat {xOM'} = {90^ \circ } + \widehat {M'Oy} = {180^ \circ } - \widehat {xOM}$

Dùng máy tính, bấm SHIFT sin 0.67 =, ta được góc xấp xỉ ${42^o}$

$\Rightarrow \widehat {xOM} = {42^ \circ },\widehat {xOM'} = {180^ \circ } - {42^ \circ } = {138^ \circ }$

Vậy $\alpha  = {42^ \circ }$ hoặc $\alpha  = {138^ \circ }$