Các phép toán trên tập hợp
(A cap B = { x|x in A) và (x in B} ) (A cup B = { x|x in A) hoặc (x in B} ) (A{rm{backslash }}B = { x in A|x notin B} )
1. Lý thuyết
+ Phép giao
Tập hợp gồm các phần tử thuộc cả hai tập hợp A và B gọi là giao của hai tập hợp A và B. Kí hiệu: \(A \cap B\)
\(A \cap B = \{ x|x \in A\) và \(x \in B\} \)
+ Phép hợp
Tập hợp gồm các phần tử thuộc tập hợp A hoặc thuộc tập hợp B gọi là hợp của hai tập hợp A và B. Kí hiệu: \(A \cup B\)
\(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} \)
+ Hiệu của A và B
Tập hợp gồm các phần tử thuộc tập hợp A nhưng không thuộc B gọi là hiệu của A và B. Kí hiệu: \(A{\rm{\backslash }}B\).
\(A{\rm{\backslash }}B = \{ x \in A|x \notin B\} \)
+ Phần bù
Nếu \(A \subset B\) thì hiệu \(A{\rm{\backslash }}B\) gọi là phần bù của A trong B. Kí hiệu: \({C_B}A\)
+ Biểu đồ Ven
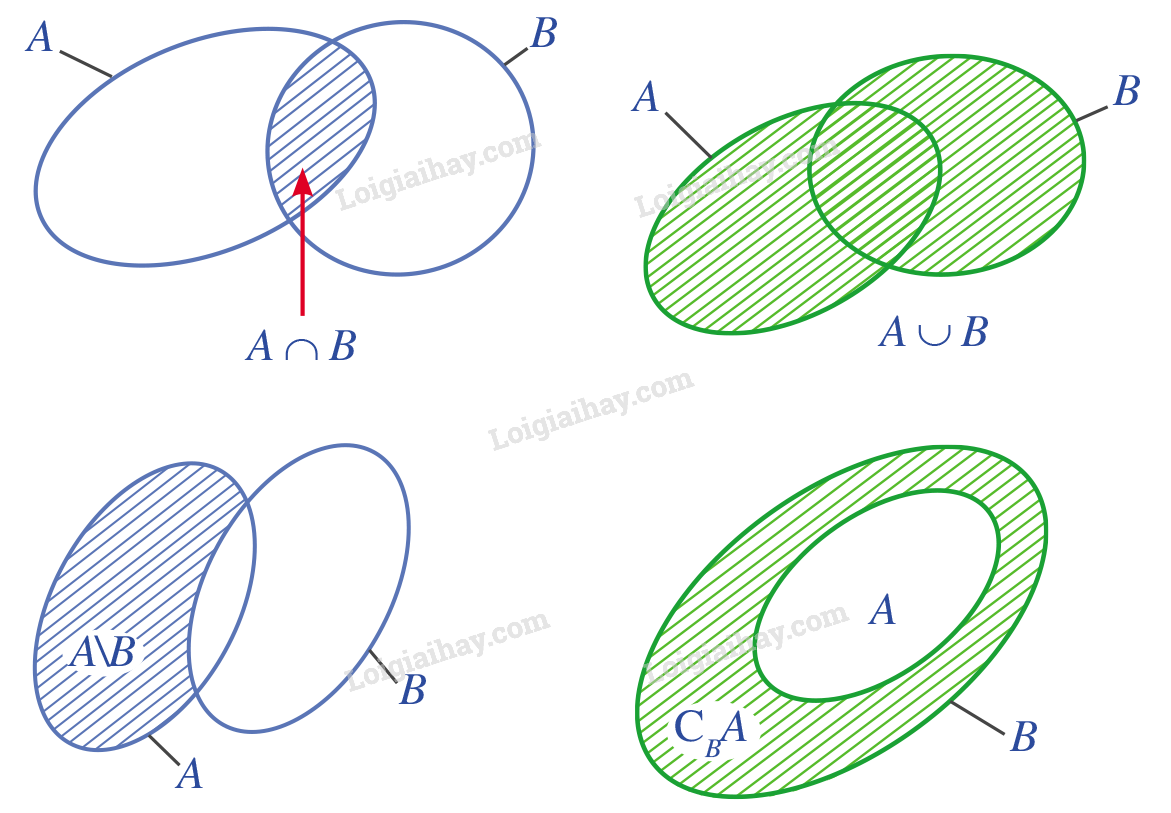
+ Mối quan hệ về số phần tử
\(n\left( {A \cup B} \right) = n(A) + n(B) - n(A \cap B)\)
\(n(A{\rm{\backslash }}B) = n(A) - n(A \cap B)\)
2. Ví dụ minh họa
Ví dụ 1. Cho hai tập hợp \(A = \left[ { - 2;{\mkern 1mu} {\mkern 1mu} 3} \right)\) và \(B = \left[ {1;6} \right)\).
Xác định các tập hợp \(A \cup B,A \cap B,A{\rm{\backslash }}B,B{\rm{\backslash }}A\)
\(A \cup B = [ - 2;6)\)

\(A \cap B = [ - 1;3)\)

\(A\backslash B = [ - 2; - 1)\)

\(B\backslash A = [3;6)\)

Ví dụ 2. Cho hai tập hợp \(A = ( - 1;4]\) và \(B = [ - 2; + \infty )\). Xác định tập hợp \({C_B}A\).
Ta có: \({C_B}A = B\backslash A = [ - 2; + \infty ){\rm{\backslash }}( - 1;4]\)

\( \Rightarrow {C_B}A = [ - 2; - 1] \cup (4; + \infty ).\)