Bài 26 trang 76 SGK Toán 9 tập 2
Cho AB, BC, CA là ba dây của đường tròn (O).
Đề bài
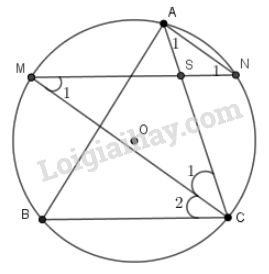
Cho \(AB, BC, CA \) là ba dây của đường tròn \((O)\). Từ điểm chính giữa \(M\) của \(\overparen{AB}\) vẽ dây \(MN\) song song với dây \(BC\). Gọi giao điểm của \(MN\) và \(AC\) là \(S\). Chứng minh \(SM = SC\) và \(SN = SA\)
Phương pháp giải - Xem chi tiết
Ta sử dụng các kiến thức sau:
+ Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
+ Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
Từ đó chỉ ra các góc bằng nhau để có tam giác \(SMC,SAN\) cân, suy ra các cặp cạnh bằng nhau.
Lời giải chi tiết
Ta có:
Vì M là điểm nằm chính giữa của \(\overparen{AB}\) nên \(\overparen{BM}=\overparen{AM}\)
+) Chứng minh SM = SC
Vì MN // BC nên \(\widehat {{M_1}} = \widehat {{C_2}}\) (2 góc so le trong)
Trong đường tròn (O): \(\widehat{{{C}_{1}}}=\widehat{{{C}_{2}}}\) (2 góc nội tiếp chắn 2 cung bằng nhau \(\overparen{BM}=\overparen{AM}\) )
Nên suy ra \(\widehat{{{M}_{1}}}=\widehat{{{C}_{1}}}\)
Suy ra tam giác SMC là tam giác cân tại S. Vậy \(SM = SC.\)
+) Chứng minh SA = SN
Trong đường tròn (O):
\(\widehat {{M_1}} = \widehat {{A_1}}\)( 2 góc nội tiếp cùng chắn cung NC)(1)
\(\widehat {{C_1}} = \widehat {{N_1}}\)(2 góc nội tiếp cùng chắn cung AM)(2)
Mà \(\widehat{{{M}_{1}}}=\widehat{{{C}_{1}}}\) (chứng minh trên)(3)
Từ (1),(2) và (3) \(\Rightarrow\) \(\widehat{{{A}_{1}}}=\widehat{{{N}_{1}}}\)
Vậy tam giác SAN cân tại S. Nên \(SA = SN\) (đpcm)