Bài 5.6 trang 109 SGK Toán 11 tập 1 - Kết nối tri thức
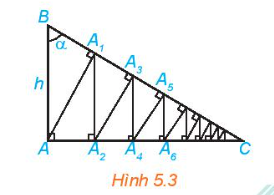
Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng (alpha ) (H.5.3). Từ A kẻ (A{A_1} bot BC), từ ({A_1}) kẻ ({A_1}{A_2} bot AC), sau đó lại kẻ ({A_2}{A_3} bot BC). Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn (A{A_1}{A_2}{A_3} ldots ) Tính độ dài đường gấp khúc này theo h và (alpha )
Đề bài
Cho tam giác vuông ABC vuông tại A , có AB = h và góc B bằng \(\alpha \) (H.5.3). Từ A kẻ \(A{A_1} \bot BC\), từ \({A_1}\) kẻ \({A_1}{A_2} \bot AC\), sau đó lại kẻ \({A_2}{A_3} \bot BC\). Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn \(A{A_1}{A_2}{A_3} \ldots \) Tính độ dài đường gấp khúc này theo h và \(\alpha \)
Phương pháp giải - Xem chi tiết
Dựa vào đề bài để tìm ra công thức tổng quát.
Lời giải chi tiết
Độ dài đường gấp khúc tạo thành cấp số nhân với số hạng tổng quát là:
\({u_n} = sin\;\alpha \; \times h \times {\left( {sin\;\alpha \;} \right)^{n - 1}}\).
Độ dài đường gập khúc: \(A{A_1} + {A_2}{A_3} + \ldots \).
Đây là tổng cấp số nhân lùi vô hạn với \({u_1} = sin\;\alpha \; \times h,\;q = sin\;\alpha \;\).
Nên \(A{A_1} + {A_2}{A_3} + \ldots = \frac{{sin\;\alpha \; \times h}}{{1 - sin\;\alpha \;}}\).