Bài 54 trang 63 SGK Toán 9 tập 2 — Không quảng cáo

Đề bài

Vẽ đồ thị của hàm số $\displaystyle y = {1 \over 4}{x^2}$ và $\displaystyle y =  - {1 \over 4}{x^2}$ trên cùng một hệ trục tọa độ

a) Qua điểm $B(0; 4)$ kẻ đường thẳng song song với trục Ox. Nó cắt đồ thị của hàm số $\displaystyle y = {1 \over 4}{x^2}$ tại hai điểm M và M’. Tìm hoành độ của M và M’.

b) Tìm trên đồ thị của hàm số $\displaystyle y =  - {1 \over 4}{x^2}$ điểm N có cùng hoành độ với M, điểm N’ có cùng hoành độ với M’. Đường thẳng NN’ có song song với Ox không? Vì sao? Tìm tung độ của N và N’ bằng hai cách:

- Ước lượng trên hình vẽ:

- Tính toán theo công thức.

Lời giải chi tiết

Vẽ đồ thị hàm số:

* Hàm số $\displaystyle y = {1 \over 4}{x^2}$ và $\displaystyle y =  - {1 \over 4}{x^2}$

- Tập xác định $D = R$

- Bảng giá trị

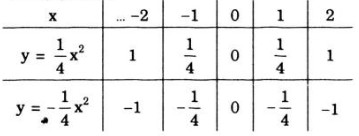
- Đồ thị hàm số $\displaystyle y = {1 \over 4}{x^2}$ và $\displaystyle y =  - {1 \over 4}{x^2}$ là các Parabol có đỉnh là gốc tọa độ O và nhận Oy làm trục đối xứng. Đồ thị hàm số $\displaystyle y = {1 \over 4}{x^2}$ nằm trên trục hoành, đồ thị hàm số $\displaystyle y =  - {1 \over 4}{x^2}$ nằm dưới trục hoành.

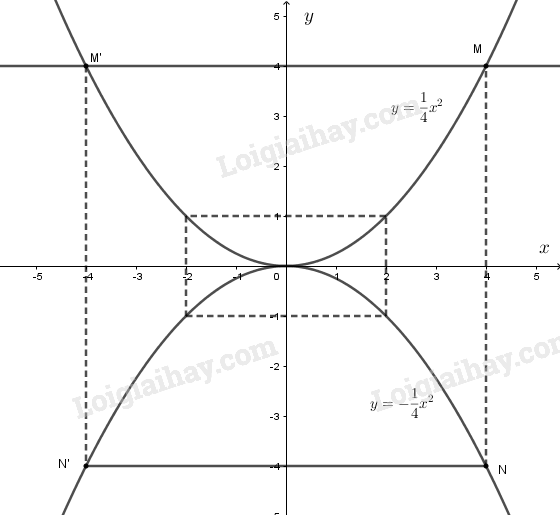
a) Đường thẳng qua $B(0; 4)$ song song với $Ox$  có dạng: y = 4.

Phương trình hoành độ giao điểm của đường thẳng y = 4 và đồ thị hàm số $\displaystyle y = {1 \over 4}{x^2}$ là:

$\dfrac{1}{4}{x^2} = 4 \Leftrightarrow {x^2} = 16 \Leftrightarrow x =  \pm 4$

Từ đó ta có hoành độ của $M$ là $x = 4$, của $M'$ là $x = - 4$.

b) Trên đồ thị hàm số $\displaystyle y =  - {1 \over 4}{x^2}$ ta xác định được điểm $N$ và $N’$ có cùng hoành độ với $M, M’$. Ta được đường thẳng $NN'//Ox$

Tìm tung độ của $N, N’$

- Ước lượng trên hình vẽ được tung độ của $N$ là $y = - 4$; của $N’$ là $y = -4$

- Tính toán theo công thức:

Điểm $N(4;y)$.  Thay $x = 4$ vào $\displaystyle y =  - {1 \over 4}{x^2}$ nên $\displaystyle y =  - {1 \over 4}{.4^2} =  - 4$

Điểm $N’(-4;y)$. Thay $x = - 4$ vào  $\displaystyle y =  - {1 \over 4}{x^2}$ nên $\displaystyle y =  - {1 \over 4}.{( - 4)^2} =  - 4$

Vậy tung độ của $N, N’$ cùng bằng $-4$.