Bài 59 trang 90 SGK Toán 9 tập 2
Cho hình bình hành ABCD
Đề bài
Cho hình bình hành \(ABCD.\) Đường tròn đi qua ba đỉnh \(A, \, B, \, C\) cắt đường thẳng \(CD\) tại \(P\) khác \(C.\) Chứng minh \(AP = AD.\)
Phương pháp giải - Xem chi tiết
+) Số đo tổng hai góc đối diện của tứ giác nội tiếp bằng \(180^0.\)
+) Sử dụng tính chất hai đường thẳng song song, tính chất hình bình hành.
Lời giải chi tiết
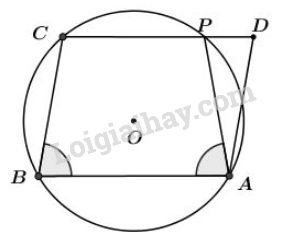
Cách 1:
Do tứ giác \(ABCP\) nội tiếp nên \(\widehat{BAP} + \widehat{BCP} = 180^0.\) (1)
Mà CD // AB nên \(\widehat{ABC}+ \widehat{BCP}= 180^0\) (hai góc trong cùng phía). (2)
Từ (1) và (2) \(\Rightarrow\) \(\widehat{BAP}= \widehat{ABC}.\)
Mà CP // AB (do CD // AB) nên \(ABCP\) là hình thang
Nên \(ABCP\) là hình thang cân (Dấu hiệu nhận biết)
\(\Rightarrow\) \(AP = BC.\) (Tính chất hình thang cân) (3)
Mà \(BC = AD\) (do ABCD là hình bình hành) (4)
Từ (3) và (4) \(\Rightarrow\) \(AP = AD\) (đpcm).
Cách 2:
Vì ABCP là tứ giác nội tiếp nên \(\widehat{ABC}+ \widehat{APC}= 180^0\)
Mà ABCD là hình bình hành nên \(\widehat {ABC} = \widehat {ADC}\) (Tính chất hình bình hành)
Hơn nữa, \(\widehat {APC} + \widehat {APD} = {180^0}\) (2 góc kề bù)
\( \Rightarrow \widehat {APD} = \widehat {ADC}\)
\(\Rightarrow\) Tam giác ADP cân tại A
\(\Rightarrow\) AP = AD (đpcm)