Bài 72 trang 96 SGK Toán 9 tập 2
Bánh xe của một ròng rọc có chu vi là 540mm
Đề bài
Bánh xe của một ròng rọc có chu vi là \(540mm\). Dây cua-roa bao bánh xe theo cung \(AB\) có độ dài \(200mm\). Tính góc \(AOB\) (h.56)
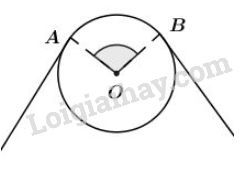
Phương pháp giải - Xem chi tiết
+) Sử dụng công thức tính chu vi đường tròn có bán kính \(R\) là \(C = 2\pi R \Rightarrow R = \dfrac{C}{{2\pi }}\)
+) Sử dụng công thức tính độ dài cung \(l = \dfrac{{\pi Rn}}{{180}}\) với \(n^\circ \) là số đo cung và \(R\) là bán kính đường tròn.
Từ đó suy ra số đo cung \(AB\) và góc \(AOB\).
Lời giải chi tiết
Chu vi bánh xe là \(C = 540mm\) nên bán kính bánh xe \(R = \dfrac{C}{{2\pi }} = \dfrac{{540}}{{2\pi }}\)\( = \dfrac{{270}}{\pi }\,\left( {mm} \right)\)
Cách 1: Cung \(AB\) có độ dài \(200mm\) và có số đo \(n^\circ \) nên độ dài \({l_{\overparen {AB}}} = \dfrac{{\pi Rn}}{{180}} \Rightarrow n = \dfrac{{180.{l_{\overparen {AB}}}}}{{\pi R}}\)\( = \dfrac{{180.200}}{{\pi .\dfrac{{270}}{\pi }}} = \dfrac{{400}}{3} \approx 133\)
Vậy \(\widehat {AOB} \approx 133^\circ \) (góc ở tâm chắn cung \(AB\)).
Cách 2: Vì góc ở tâm chắn cung và độ dài cung là 2 đại lượng tỉ lệ thuận nên
\(\frac{\widehat {AOB}}{360^0}=\frac{l_{\overparen {AB}}}{C}\) nên \(\frac{\widehat {AOB}}{360^0}=\frac{200}{540}\)\(\Rightarrow\) \(\widehat {AOB} \approx 133^\circ \)