Câu 28 trang 112 SGK Hình học 11 Nâng cao
Cho tam giác ABC và mặt phẳng (P). Biết góc giữa mp(P) và mp(ABC) là φ (φ ≠ 90˚); hình chiếu của tam giác ABC trên mp(P) là tam giác A’B’C’. Chứng minh rằng
Cho tam giác ABC và mặt phẳng (P). Biết góc giữa mp(P) và mp(ABC) là φ (φ ≠ 90˚); hình chiếu của tam giác ABC trên mp(P) là tam giác A’B’C’. Chứng minh rằng
\({S_{A'B'C'}} = {S_{ABC}}.\cos \varphi \)
Hướng dẫn. Xét hai trường hợp :
a) Tam giác ABC có 1 cạnh song song hoặc nằm trong mp(P).
b) Tam giác ABC không có cạnh nào song song hay nằm trong mp(P).
LG a
Tam giác ABC có một cạnh song song hoặc nằm trong mp(P)
Lời giải chi tiết:
Xét trường hợp tam giác ABC có một cạnh, chẳng hạn BC nằm trong mp(P). Gọi A’ là hình chiếu của A trên mp(P).
Kẻ đường cao A’H của tam giác A’BC (H ϵ BC) thì AH là đường cao của tam giác ABC và \(\widehat {AHA'} = \varphi ,A'H = AH\cos \varphi .\)
Ta có: \({S_{A'BC}} = {1 \over 2}BC.A'H \) \(= {1 \over 2}BC.AH\cos \varphi = {S_{ABC.cos\varphi }}\)
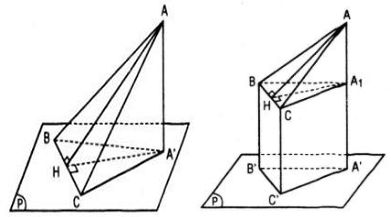
Trường hợp cạnh BC của tam giác ABC song song với mp(P). Xét mp(Q) chứa BC và song song với mp(P), gọi giao điểm của AA’ với mp(Q) là A 1 . Khi đó ta có ΔA 1 BC = ΔA’B’C’ ; góc giữa mp(ABC) và mp(Q) bằng φ.
Do đó : \({S_{A'B'C'}} = {S_{{A_1}BC}} = {S_{ABC }.\cos \varphi}\)
LG b
Tam giác ABC không có cạnh nào song song hay nằm trong mp(P).
Lời giải chi tiết:
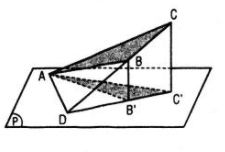
Xét trường hợp tam giác ABC không có cạnh nào song song hay nằm trong mp(P).
Ta có thể giả sử mp(P) đi qua điểm A sao cho các đỉnh B, C ở về cùng một phía đối với mp(P).
Gọi D là giao điểm của đường thẳng BC và mp(P); B’, C’ lần lượt là hình chiếu của B, C trên (P) thì B’C’ đi qua D.
Khi đó theo trường hợp a ta có :
\(\eqalign{ & {S_{ADC'}} = {S_{ADC.\cos \varphi }} \cr & {S_{ADB'}} = {S_{ABD.\cos \varphi }} \cr} \)
Trừ từng vế hai đẳng thức trên, ta có :
\({S_{AB'C'}} = {S_{ABC.\cos \varphi }}\)
Vậy mọi trường hợp ta đều có :
\({S_{A'B'C'}} = {S_{ABC.\cos \varphi }}\)