Đề kiểm tra 45 phút (1 tiết) - Đề số 3 - Chương 3 - Hình học 9
Giải Đề kiểm tra 45 phút (1 tiết) - Đề số 3 - Chương 3 - Hình học 9
Đề bài
Bài 1: Cho tam giác ABC nội tiếp đường tròn (O) đường kính BC. Tia phân giác của góc BAC cắt đường tròn tại D.
a) Chứng tỏ \(OD \bot BC.\)
b) Gọi I là tâm đường tròn nội tiếp ∆ABC. Tính góc BIC.
Bài 2: Từ một điểm A ở bên ngoài đường tròn (O), vẽ hai tiếp tuyến AB, AC đến đường tròn ( B và C là các tiếp điểm). Từ C vẽ đường thẳng vuông góc với AB cắt AB tại D và cắt (O) tại E. Từ E vẽ EF vuông góc với BC ( F thuộc BC) và EH vuông góc với AC ( H thuộc AC).
a) Chứng minh : \(\widehat {DEF} = \widehat {FEH}.\)
b) Chứng minh : \(EF^2 = ED.EH.\)
c) Gọi N là giao điểm của DF và EB, M là giao điểm của FH và EC. Chứng tỏ rằng tứ giác MENF nội tiếp.
d) Cho \(\widehat {BAC} = 30^\circ \). Tính độ dài cung nhỏ BC và diện tích hình quạt tròn giới hạn bởi hai bán kính OB và OC.
LG bài 1
Phương pháp giải:
Sử dụng:
+Đường kính đi qua điểm chính giữa của dây cung thì vuông góc với dây căng cung ấy
+Tổng ba góc của 1 tam giác bằng 180 độ
Lời giải chi tiết:
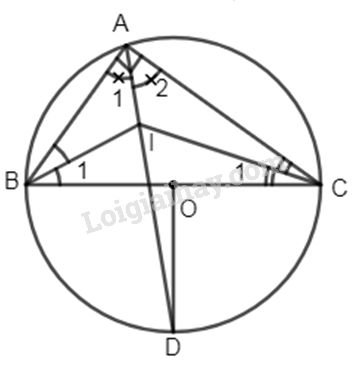
a) Ta có \(\widehat {{A_1}} = \widehat {{A_2}}\) (gt) \( \Rightarrow \overparen{ DB} = \overparen{ DC}\)
\( \Rightarrow OD \bot BC\) ( đường kính đi qua điểm chính giữa của dây cung).
b) Ta có \(\widehat A + \widehat B + \widehat C = 180^\circ \)
\( \Rightarrow \widehat B + \widehat C = 180^\circ - \widehat A\)\(\, = 180^\circ - 90^\circ = 90^\circ \) (\(\widehat A = 90^\circ \) vì BC là đường kính).
\( \Rightarrow \dfrac{{\widehat B} }{ 2} + \dfrac{{\widehat C} }{ 2} = 45^\circ \) hay \(\widehat {{B_1}} + \widehat {{C_1}} = 45^\circ \)
Trong ∆BIC có :
\(\widehat {BIC} = 180^\circ - \left( {\widehat {{B_1}} + \widehat {{C_1}}} \right)\)\(\, = 180^\circ - 45^\circ = 135^\circ \).
LG bài 2
Phương pháp giải:
Sử dụng:
+Tính chất 2 tiếp tuyến cắt nhau
+Tính chất tứ giác nội tiếp
+Hai góc nội tiếp cùng chắn 1 cung thì bằng nhau
+Góc nội tiếp bằng góc giữa tiếp tuyến và dây cùng chắn 1 cung
+Tổng ba góc của 1 tam giác bằng 180 độ
+Công thức
\({l} =\dfrac{{\pi R.n} }{ {180}} \)
\({S_q} = \dfrac{{\pi {R^2}.n} }{ {360}}\)
Lời giải chi tiết:
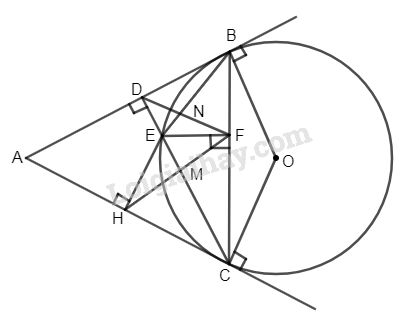
a) Ta có tứ giác BDEF nội tiếp ( vì \(\widehat {BDE} + \widehat {{\rm{BF}}E} = 180^\circ \))
\( \Rightarrow \widehat {BDF} + \widehat {{\rm{DEF}}} = 180^\circ \)
Tương tự tứ giác CHEF nội tiếp \( \Rightarrow \widehat {HCF} + \widehat {FEH} = 180^\circ \)
Mà \(\widehat {DBF} = \widehat {HCF}\) (tính chất hai tiếp tuyến cắt nhau)
Do đó \(\widehat {{\rm{DEF}}} = \widehat {FEH}\) (1)
b) Ta có \(\widehat {EDF} = \widehat {EBF}\) ( góc nội tiếp cùng chắn cung EF)
\(\widehat {EBF} = \widehat {ECH}\) (góc nội tiếp bằng góc giữa tiếp tuyến và một dây cùng chắn cung EC)
\(\widehat {ECH} = \widehat {EFH}\) ( góc nội tiếp cùng chắn cung EH)
Do đó \(\widehat {EDF} = \widehat {EFH}\) (2)
Từ (1) và (2), ta có :
∆EFD và ∆EHF đồng dạng (g.g)
\( \Rightarrow \dfrac{{EF} }{ {EH}} = \dfrac{{ED}}{{EH}} \Rightarrow E{H^2} = ED.EH\).
c) Ta có \(\widehat {EFM} = \widehat {EBC}\) (cmt),
\(\widehat {NFE} = \widehat {BCE}\) (cmt)
mà \(\widehat {NEM} + \widehat {BCE} + \widehat {EBC} = 180^\circ \) ( tổng ba góc của tam giác)
\( \Rightarrow \widehat {NEM} + \widehat {NEF} + \widehat {EFM} = 180^\circ \) hay \(\widehat {NEM} + \widehat {NFM} = 180^\circ \)
Do đó tứ giác MENF nội tiếp.
d) Dễ thấy tứ giác ABOC nội tiếp (\(\widehat {ABO} + \widehat {ACO} = 180^\circ \))
\( \Rightarrow \widehat {BAC} + \widehat {BOC} = 180^\circ \) mà \(\widehat {BAC} = 30^\circ \Rightarrow \widehat {BOC} = 150^\circ \)
Vậy \({l_{\overparen{BC}}} =\dfrac{{\pi R.150} }{ {180}} = \dfrac{{5\pi R}}{ 5}\) và \({S_q} = \dfrac{{\pi {R^2}.150} }{ {360}} = \dfrac{{5\pi {R^2}}}{ {12}}.\)