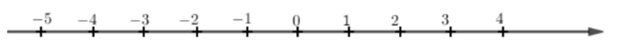Đề kiểm tra học kì 1 Toán 6 Chân trời sáng tạo - Đề số 1
Đề bài
-
A.
\(a \ge 0\)
-
B.
\(a > 0\)
-
C.
\(a < 0\)
-
D.
\(a \le 0\)
Xác định số nhỏ nhất khác 0 trong các bội chung của 2 và 3.
-
A.
0
-
B.
6
-
C.
2
-
D.
3
-
A.
\(a\) là ước của \(a\)
-
B.
\(a\) là bội của \(a\)
-
C.
0 là ước của \(a\)
-
D.
1 là ước của \(a\)
Trong phép chia có dư \(a\) chia cho \(b,\) trong đó \(b \ne 0,\) ta luôn tìm được đúng hai số tự nhiên \(q\) và \(r\) duy nhất sao cho:
\(a = b.q + r\)
Khẳng định nào sau đây đúng ?
-
A.
\(r \ge b\)
-
B.
\(0 < b < r\)
-
C.
\(0 < r < b\)
-
D.
\(0 \le r < b\)
Chọn câu sai.
-
A.
$\left( { - 5} \right).25 = - 125$
-
B.
$6.\left( { - 15} \right) = - 90$
-
C.
$125.\left( { - 20} \right) = - 250$
-
D.
$225.\left( { - 18} \right) = - 4050$
Chọn câu đúng.
-
A.
\(10000 = {10^3}\)
-
B.
\({1020^0} = 0\)
-
C.
\(x.{x^7} = {x^7}\)
-
D.
\({12^7}:{12^4} = {12^3}\)
Lan tìm hiểu về thức ăn sáng nay của các bạn trong lớp và thu được kết quả như sau:

Dữ liệu nào sau đây không là số liệu?
-
A.
Xôi
-
B.
11
-
C.
8
-
D.
2
-
A.
20 cm 2
-
B.
25 cm
-
C.
20 cm
-
D.
10 cm
Chọn phát biểu sai ?
-
A.
Hình có bốn đỉnh là hình chữ nhật
-
B.
Hình chữ nhật có bốn đỉnh
-
C.
Hình chữ nhật có hai cặp cạnh đối song song.
-
D.
Hình chữ nhật có hai đường chéo bằng nhau
Viết tập hợp \(A = \left\{ {16;17;18;19} \right\}\) dưới dạng chỉ ra tính chất đặc trưng.
-
A.
\(A = \left\{ {x \in N|15 < x < 19} \right\}\)
-
B.
\(A = \left\{ {x\in N |15 < x < 20} \right\}\)
-
C.
\(A = \left\{ {x\in N |16 < x < 20} \right\}\)
-
D.
\(A = \left\{ {x\in N |15 < x \le 20} \right\}\)
5 là phần tử của
-
A.
Ư\(\left( {14} \right)\)
-
B.
Ư\(\left( {15} \right)\)
-
C.
Ư\(\left( {16} \right)\)
-
D.
Ư\(\left( {17} \right)\)
Khẳng định nào là sai:
-
A.
$0$ và $1$ không là số nguyên tố cũng không phải hợp số.
-
B.
Cho số $a > 1$, $a$ có $2$ ước thì $a$ là hợp số.
-
C.
$2$ là số nguyên tố chẵn duy nhất.
-
D.
Số nguyên tố là số tự nhiên lớn hơn $1$ mà chỉ có hai ước là $1$ và chính nó.
Tập hợp số tự nhiên được kí hiệu là
-
A.
\(N\)
-
B.
\({N^*}\)
-
C.
\(\left\{ N \right\}\)
-
D.
\(Z\)
Nếu số bạn lớp 6B tăng thêm một bạn và bạn đó thích mận thì cột mận tăng thêm bao nhiêu đơn vị?
-
A.
6
-
B.
1
-
C.
7
-
D.
2
Tìm chu vi hình tứ giác MNPQ có bốn cạnh bằng nhau, biết cạnh MN = 4cm.
-
A.
16 dm
-
B.
16 mm
-
C.
12 cm
-
D.
16 cm
-
A.
Phép cộng của 1 và 2
-
B.
Phép trừ của 3 và 2
-
C.
Phép cộng của 1 và 3
-
D.
Phép trừ của 3 và 1
Điều tra loại phim yêu thích nhất của 36 học sinh lớp 6A3, bạn lớp trưởng thu được bảng dữ liệu ban đầu như sau:

Viết tắt: H: Hoạt hình; L: Lịch sử; K: Khoa học; C: Ca nhạc; T: Trinh thám.
Loại phim nào được các bạn học sinh lớp 6A3 yêu thích nhất?
-
A.
Hoạt hình
-
B.
Lịch sử
-
C.
Khoa học
-
D.
Trinh thám
Tính \(125 - 200\)
-
A.
$ - 75$
-
B.
$75$
-
C.
$ - 85$
-
D.
$85$
Số 40 được phân tích thành các thừa số nguyên tố là:
-
A.
\(40 = 4.10\)
-
B.
\(40 = 2.20\)
-
C.
\(40 = {2^2}.5\)
-
D.
\(40 = {2^3}.5\)
Chọn khẳng định đúng:
-
A.
Mọi số tự nhiên đều có ước chung với nhau.
-
B.
Mọi số tự nhiên đều có ước là 0
-
C.
Số nguyên tố chỉ có đúng $1$ ước là chính nó.
-
D.
Hai số nguyên tố khác nhau thì không có ước chung
Phép tính \(x - 5\) thực hiện được khi
-
A.
\(x < 5\)
-
B.
\(x \ge 5\)
-
C.
\(x < 4\)
-
D.
\(x = 3\)
-
A.
\(4\)
-
B.
\( - 7\)
-
C.
\(7\)
-
D.
\(6\)
Cho \(E = \left\{ {3;\, - 8;\,0} \right\}\) . Tập hợp F gồm các phần tử của E và các số đối của chúng là?
-
A.
\(F = \left\{ {3;\,8;\;\,0;\, - 3} \right\}\)
-
B.
\(F = \left\{ { - 3;\, - 8;\,\;0} \right\}\)
-
C.
\(F = \left\{ {3;\, - 8;\,\;0;\, - 3} \right\}\;\)
-
D.
\(F = \left\{ {3;\, - 8;\,\;0;\, - 3;\,\;8} \right\}\)
\(\overline {a001} \left( {a \ne 0} \right)\) bằng
-
A.
\(\overline {a001} = a \times 1000 + 0 \times 100 + 0 \times 10 + 1\)
-
B.
\(\overline {a001} = 1000 + 0 \times 100 + 0 \times 10 + 1\)
-
C.
\(\overline {a001} = a \times 1000 + 1 \times 100\)
-
D.
\(\overline {a001} = a + 0 + 0 + 1\)
Số nào trong các số sau không là số nguyên tố?
-
A.
2
-
B.
3
-
C.
5
-
D.
9
Số tự nhiên \(m\) nào dưới đây thỏa mãn \({20^{2018}} < {20^m} < {20^{2020}}?\)
-
A.
\(m = 2020\)
-
B.
\(m = 2018\)
-
C.
\(m = 2019\)
-
D.
\(m = 20\)
Trong một cuộc thi có \(20\) câu hỏi. Mỗi câu trả lời đúng được \(10\) điểm, mỗi câu trả lời sai bị trừ \(3\) điểm. Một học sinh đạt được \(148\) điểm. Hỏi bạn đã trả lời đúng bao nhiêu câu hỏi?
-
A.
$16$
-
B.
$15$
-
C.
$4$
-
D.
$10$
Chọn câu sai.
-
A.
Tổng ba số tự nhiên liên tiếp chia hết cho \(3\)
-
B.
Tổng bốn số tự nhiên liên tiếp không chia hết cho \(4\)
-
C.
Tổng năm số tự nhiên chẵn liên tiếp chia hết cho \(10\)
-
D.
Tổng bốn số tự nhiên liên tiếp chia hết cho \(4\)
Cho số \(A = \overline {a785b} \) . Tìm tổng các chữ số $a$ và $b$ sao cho $A$ chia $9$ dư $2.$
-
A.
\(\left( {a + b} \right) \in \left\{ {9;18} \right\}\)
-
B.
\(\left( {a + b} \right)\in \left\{ {0;9;18} \right\}\)
-
C.
\(\left( {a + b} \right) \in \left\{ {1;2;3} \right\}\)
-
D.
\(\left( {a + b} \right)\in \left\{ {4;5;6} \right\}\)
Một căn phòng hình chữ nhật dài $680$cm, rộng $480$cm. Người ta muốn lát kín căn phòng đó bằng gạch hình vuông mà không có viên gạch nào bị cắt xén. Hỏi viên gạch có độ dài lớn nhất là bao nhiêu?
-
A.
$5\,cm$
-
B.
$10\,cm$
-
C.
$20\,cm$
-
D.
$40\,cm$
-
A.
\( - 2021;\,\, - 10;\,\,4;\,0;\, - 1\)
-
B.
\( - 2021;\,\, - 10;\,\, - 1;\,\,0;\,\,4\)
-
C.
\( - 2021;\,\, - 10;\,\,0;\,\, - 1;\,\,4\)
-
D.
\(4;\,0;\, - 1;\, - 10;\, - 2021\)
Tổng các số nguyên âm nhỏ nhất có $3$ chữ số và số nguyên âm lớn nhất có $3$ chữ số là:
-
A.
\( - 1099\)
-
B.
\(1099\)
-
C.
\( - 1009\)
-
D.
\( - 1199\)
Cho \(A = \left( {135 - 35} \right).\left( { - 47} \right) + 53.\left( { - 48 - 52} \right)\) và \(B = 25.\left( {75 - 49} \right) + 75.\left| {25 - 49} \right|.\)
Chọn câu đúng.
-
A.
\(A\) và \(B\) đối nhau
-
B.
\(A\) và \(B\) bằng nhau
-
C.
\(A\) và \(B\) cùng dấu
-
D.
\(A\) và \(B\) trái dấu
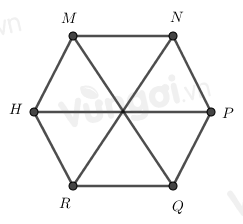
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
-
A.
8
-
B.
2
-
C.
4
-
D.
6
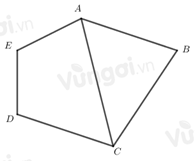
Cho chu vi tứ giác ACDE bằng 45 cm, chu vi tam giác ABC bằng 32 cm, AC = 10 cm. Khi đó chu vi hình ABCDE là:
-
A.
77 cm
-
B.
67 cm
-
C.
57 cm
-
D.
87 cm
Biểu đồ tranh dưới đây cho biết số học sinh nữ của các lớp khối 6 trường THCS Hoàng Việt.
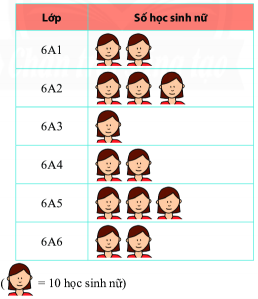
Em hãy quan sát biểu đồ tranh ở trên và chọn đáp án đúng
-
A.
Lớp 6A1 có ít học sinh nữ nhất
-
B.
Lớp 6A4 có nhiều học sinh nữ hơn lớp 6A5
-
C.
Lớp 6A6 có 20 học sinh nữ.
-
D.
Tổng số học sinh nữ của các lớp khối 6 là 120 học sinh
Tìm số \(\overline {xy} \) biết \(\overline {xy} .\overline {xyx} = \overline {xyxy} \)
-
A.
\(10\)
-
B.
\(11\)
-
C.
\(12\)
-
D.
\(13\)
Cho \(C = 1 + 3 + {3^2} + {3^3} + ... + {3^{11}}\) . Khi đó \(C\) chia hết cho số nào dưới đây?
-
A.
\(9\)
-
B.
\(11\)
-
C.
\(13\)
-
D.
\(12\)
Cho hình bình hành có chu vi là 480cm, có độ dài cạnh đáy gấp 5 lần cạnh kia và gấp 8 lần chiều cao. Tính diện tích hình bình hành
-
A.
5000 cm
-
B.
10000 cm
-
C.
2500 cm 2
-
D.
5000 cm 2
Tìm các giá trị thích hợp của chữ số $a$ sao cho: \( - \overline {a99} > - 649 > - \overline {6a0} \)
-
A.
$6$
-
B.
$5$
-
C.
$4$
-
D.
$7$
Lời giải và đáp án
-
A.
\(a \ge 0\)
-
B.
\(a > 0\)
-
C.
\(a < 0\)
-
D.
\(a \le 0\)
Đáp án : B
Xác định số nhỏ nhất khác 0 trong các bội chung của 2 và 3.
-
A.
0
-
B.
6
-
C.
2
-
D.
3
Đáp án : B
Tìm B(2), B(3): Muốn tìm bội của một số tự nhiên ta lấy số đó nhân lần lượt với các số 0; 1; 2; 3…
Tìm BC(2,3)
Tìm số nhỏ nhất khác 0 trong các bội chung vừa tìm được.
B(2)={0;2;4;6;8;...}
B(3)={0;3;6;9;...}
Số nhỏ nhất khác 0 trong bội chung của 2 và 3 là: 6.
-
A.
\(a\) là ước của \(a\)
-
B.
\(a\) là bội của \(a\)
-
C.
0 là ước của \(a\)
-
D.
1 là ước của \(a\)
Đáp án : C
Lý thuyết ước và bội
Nếu có số tự nhiên \(a\) chia hết cho số tự nhiên \(b\) thì ta nói \(a\) là bội của \(b,\) còn \(b\) là ước của \(a.\)
Đáp án C sai vì không có số nào chia được cho 0.
0 không bao giờ là ước của một số tự nhiên bất kì.
Trong phép chia có dư \(a\) chia cho \(b,\) trong đó \(b \ne 0,\) ta luôn tìm được đúng hai số tự nhiên \(q\) và \(r\) duy nhất sao cho:
\(a = b.q + r\)
Khẳng định nào sau đây đúng ?
-
A.
\(r \ge b\)
-
B.
\(0 < b < r\)
-
C.
\(0 < r < b\)
-
D.
\(0 \le r < b\)
Đáp án : C
Định nghĩa về phép chia hết và phép chia có dư.
Khi chia a cho b, trong đó \(b \ne 0,\) ta luôn tìm được đúng hai số tự nhiên \(q\) và \(r\) duy nhất sao cho:
\(a = b.q + r\) trong đó \(0 \le r < b\)
Phép chia a cho b là phép chia có dư nên \(r \ne 0\)
Vậy \(0 < r < b\) .
Chọn câu sai.
-
A.
$\left( { - 5} \right).25 = - 125$
-
B.
$6.\left( { - 15} \right) = - 90$
-
C.
$125.\left( { - 20} \right) = - 250$
-
D.
$225.\left( { - 18} \right) = - 4050$
Đáp án : C
Tính toán các kết quả của từng đáp án rồi kết luận:
Muốn nhân hai số nguyên khác dấu, ta nhân hai giá trị tuyệt đối của chúng rồi đặt dấu $\left( - \right)$ trước kết quả nhận được.
Đáp án A: $\left( { - 5} \right).25 = - 125$ nên $A$ đúng.
Đáp án B: $6.\left( { - 15} \right) = - 90$ nên \(B\) đúng.
Đáp án C: $125.\left( { - 20} \right) = - 2500 \ne - 250$ nên \(C\) sai.
Đáp án D: $225.\left( { - 18} \right) = - 4050$ nên \(D\) đúng.
Chọn câu đúng.
-
A.
\(10000 = {10^3}\)
-
B.
\({1020^0} = 0\)
-
C.
\(x.{x^7} = {x^7}\)
-
D.
\({12^7}:{12^4} = {12^3}\)
Đáp án : D
Dựa vào quy tắc nhân, chia hai lũy thừa cùng cơ số: \({a^m}.{a^n} = {a^{m + n}}\,\,\,\left( {m;n \in N} \right);\)\(\,\,{a^m}:{a^n} = {a^{m - n}}\,\,\,\left( {a \ne 0;m \ge n} \right)\)
Ta có:
\(\begin{array}{l}10000 = {10^4}\\{1020^0} = 1\\x.{x^7} = {x^{1 + 7}} = {x^8}\\{12^7}:{12^4} = {12^{7 - 4}} = {12^3}\end{array}\)
Do đó chỉ có đáp án D đúng.
Lan tìm hiểu về thức ăn sáng nay của các bạn trong lớp và thu được kết quả như sau:

Dữ liệu nào sau đây không là số liệu?
-
A.
Xôi
-
B.
11
-
C.
8
-
D.
2
Đáp án : A
Số liệu là các số.
Xôi không là số nên không là số liệu.
-
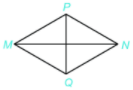
A.
20 cm 2
-
B.
25 cm
-
C.
20 cm
-
D.
10 cm
Đáp án : C
Chu vi hình thoi MPNQ là: 4.5 = 20 (cm)
Chọn phát biểu sai ?
-
A.
Hình có bốn đỉnh là hình chữ nhật
-
B.
Hình chữ nhật có bốn đỉnh
-
C.
Hình chữ nhật có hai cặp cạnh đối song song.
-
D.
Hình chữ nhật có hai đường chéo bằng nhau
Đáp án : A
Sử dụng dấu hiệu nhận biết hình chữ nhật
Hình chữ nhật có bốn đỉnh, hai cặp cạnh đối song song, hai đường chéo bằng nhau.
=> Đáp án B, C, D đúng.
Hình có 4 đỉnh chưa chắc là hình chữ nhật ví dụ:
Viết tập hợp \(A = \left\{ {16;17;18;19} \right\}\) dưới dạng chỉ ra tính chất đặc trưng.
-
A.
\(A = \left\{ {x \in N|15 < x < 19} \right\}\)
-
B.
\(A = \left\{ {x\in N |15 < x < 20} \right\}\)
-
C.
\(A = \left\{ {x\in N |16 < x < 20} \right\}\)
-
D.
\(A = \left\{ {x\in N |15 < x \le 20} \right\}\)
Đáp án : B
+ Tìm tính chất chung của các phần tử trong tập hợp
+ Viết tập hợp dưới dạng chỉ ra tính chất đặc trưng
Nhận thấy các số \(16;17;18;19\) là các số tự nhiên lớn hơn \(15\) và nhỏ hơn \(20\)
Nên \(A = \left\{ {x \in N |15 < x < 20} \right\}\).
5 là phần tử của
-
A.
Ư\(\left( {14} \right)\)
-
B.
Ư\(\left( {15} \right)\)
-
C.
Ư\(\left( {16} \right)\)
-
D.
Ư\(\left( {17} \right)\)
Đáp án : B
Ư \(\left( a \right)\) là tập hợp các ước của \(a\)
Nếu 5 là ước của \(a\) thì 5 là phần tử của Ư \(\left( a \right)\)
Ta có: Ư \(\left( {15} \right)\) là tập hợp các ước của 15.
Mà 5 là một ước của 15 nên 5 là phần tử của Ư \(\left( {15} \right)\)
Khẳng định nào là sai:
-
A.
$0$ và $1$ không là số nguyên tố cũng không phải hợp số.
-
B.
Cho số $a > 1$, $a$ có $2$ ước thì $a$ là hợp số.
-
C.
$2$ là số nguyên tố chẵn duy nhất.
-
D.
Số nguyên tố là số tự nhiên lớn hơn $1$ mà chỉ có hai ước là $1$ và chính nó.
Đáp án : B
Áp dụng định nghĩa:
+ Hợp số là một số tự nhiên có thể biểu diễn thành tích của hai số tự nhiên khác nhỏ hơn nó. Một định nghĩa khác tương đương: hợp số là số chia hết cho các số khác ngoài 1 và chính nó.
+ Số nguyên tố là số tự nhiên lớn hơn $1$ mà chỉ có hai ước là $1$ và chính nó.
+) Số $a$ phải là số tự nhiên lớn hơn \(1\) và có nhiều hơn $2$ ước thì $a$ mới là hợp số nên B sai.
+) $1$ là số tự nhiên chỉ có $1$ ước là $1$ nên không là số nguyên tố và $0$ là số tự nhiên nhỏ hơn $1$ nên không là số nguyên tố. Lại có $0$ và $1$ đều không là hợp số do đó A đúng.
+) Số nguyên tố là số tự nhiên lớn hơn $1$ mà chỉ có hai ước là $1$ và chính nó nên D đúng và suy ra $2$ là số nguyên tố chẵn duy nhất nên C đúng.
Tập hợp số tự nhiên được kí hiệu là
-
A.
\(N\)
-
B.
\({N^*}\)
-
C.
\(\left\{ N \right\}\)
-
D.
\(Z\)
Đáp án : A
Tập hợp số tự nhiên kí hiệu là N.

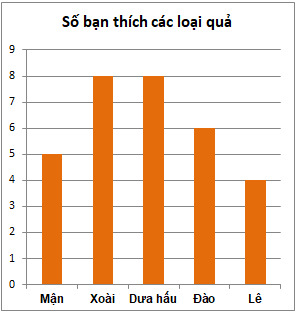
Nếu số bạn lớp 6B tăng thêm một bạn và bạn đó thích mận thì cột mận tăng thêm bao nhiêu đơn vị?
-
A.
6
-
B.
1
-
C.
7
-
D.
2
Đáp án : B
Tìm số bạn thích mận của lớp sau khi thêm một bạn.
Số bạn thích mận tăng 1 bạn nên chiều cao của cột “Mận” tăng 1 đơn vị.
Biểu đồ cột là:
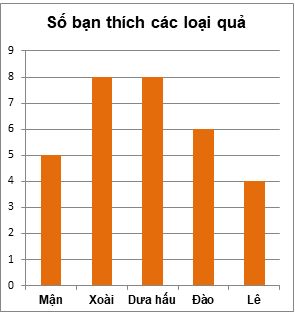
Tìm chu vi hình tứ giác MNPQ có bốn cạnh bằng nhau, biết cạnh MN = 4cm.
-
A.
16 dm
-
B.
16 mm
-
C.
12 cm
-
D.
16 cm
Đáp án : D
Chu vi của một hình tứ giác bằng tổng độ dài 4 cạnh.
Do hình tứ giác MNPQ có bốn cạnh bằng nhau và MN = 4cm nên :
Chu vi tứ giác MNPQ là: \(4 + 4 + 4 + 4 = 16\) (cm)
Cách khác:
Chu vi tứ giác MNPQ là: \(4.4 = 16\) (cm)
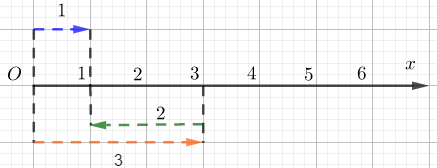
-
A.
Phép cộng của 1 và 2
-
B.
Phép trừ của 3 và 2
-
C.
Phép cộng của 1 và 3
-
D.
Phép trừ của 3 và 1
Đáp án : B
Số 3 và số 1 cùng chiều từ trái sang phải, số 2 ngược chiều với hai số này. Mà ta có 3-2=1 nên hình ảnh trên minh họa cho phép trừ 3-2.
Điều tra loại phim yêu thích nhất của 36 học sinh lớp 6A3, bạn lớp trưởng thu được bảng dữ liệu ban đầu như sau:

Viết tắt: H: Hoạt hình; L: Lịch sử; K: Khoa học; C: Ca nhạc; T: Trinh thám.
Loại phim nào được các bạn học sinh lớp 6A3 yêu thích nhất?
-
A.
Hoạt hình
-
B.
Lịch sử
-
C.
Khoa học
-
D.
Trinh thám
Đáp án : A
- Lập bảng thống kê: Điền số bạn thích vào ô bên dưới của mỗi loại phim.
- Tìm phim có số bạn thích nhiều nhất dựa vào bảng.
Số chữ H là 11, số chữ L là 6, số chữ K là 4, số chữ C là 7, số chữ T là 8.
Bảng thống kế các bộ phim yêu thích của các học sinh lớp 6A3 là:
|
Loại phim |
Hoạt hình |
Lịch sử |
Khoa học |
Ca nhạc |
Trinh thám |
|
Số bạn thích |
11 |
6 |
4 |
7 |
8 |
Phim hoạt hình có số bạn là 11 nên loại phim hoạt hình được các bạn học sinh lớp 6A3 yêu thích nhất.
Tính \(125 - 200\)
-
A.
$ - 75$
-
B.
$75$
-
C.
$ - 85$
-
D.
$85$
Đáp án : A
Muốn trừ số nguyên $a$ cho số nguyên $b,$ ta cộng $a$ với số đối của $b:$ $a - b = a + \left( { - b} \right)$
\(125 - 200 = 125 + \left( { - 200} \right)\)\( = - \left( {200 - 125} \right) = - 75\)
Số 40 được phân tích thành các thừa số nguyên tố là:
-
A.
\(40 = 4.10\)
-
B.
\(40 = 2.20\)
-
C.
\(40 = {2^2}.5\)
-
D.
\(40 = {2^3}.5\)
Đáp án : D
Sử dụng phương pháp “rẽ nhánh”:
- Tìm một ước nguyên tố của 40, là 2.
- Viết 40 thành tích của 2 với một thừa số khác: 40=2.20.
- Vẽ 2 nhánh từ số 40 cho hai số 2 và 20.
- Tiếp tục tìm ước nguyên tố của 20, là 2.
- Viết số 20 thành tích của 2 với một thừa số khác: 20=2.10.
- Vẽ 2 nhánh từ số 20 cho hai số 2 và 10.
- Viết số 10 thành tích của 2 với 5: 10=2.5
- Vẽ 2 nhánh từ số 10 cho hai số 2 và 5.
- Hai số này đều là số nguyên tố nên ta dừng lại.
- Lấy tích tất cả các thừa số ở cuối cùng mỗi nhánh.
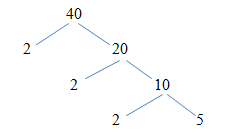
Vậy \(40 = 2.2.2.5 = {2^3}.5\)
Chọn khẳng định đúng:
-
A.
Mọi số tự nhiên đều có ước chung với nhau.
-
B.
Mọi số tự nhiên đều có ước là 0
-
C.
Số nguyên tố chỉ có đúng $1$ ước là chính nó.
-
D.
Hai số nguyên tố khác nhau thì không có ước chung
Đáp án : A
- Áp dụng kiến thức:
Mọi số tự nhiên đều có ước là $1$.
Số nguyên tố có $2$ ước là $1$ và chính nó.
Mọi số nguyên tố khác nhau đều có ước chung duy nhất là $1$.
A. Đáp án này đúng vì mọi số tự nhiên đều có ước chung là $1$
B. Đáp án này sai, vì $0$ không là ước của $1$ số nào cả.
C. Đáp án này sai, vì số nguyên tố có $2$ ước là $1$ và chính nó.
D. Đáp án này sai, vì $2$ số nguyên tố có ước chung là $1$.
Phép tính \(x - 5\) thực hiện được khi
-
A.
\(x < 5\)
-
B.
\(x \ge 5\)
-
C.
\(x < 4\)
-
D.
\(x = 3\)
Đáp án : B
Phép tính \(a - b\) thực hiện được khi \(a \ge b.\)
Phép tính \(x - 5\) thực hiện được khi \(x \ge 5.\)
-
A.
\(4\)
-
B.
\( - 7\)
-
C.
\(7\)
-
D.
\(6\)
Đáp án : C
Đếm xem điểm \( - 4\) cách điểm \(3\) bao nhiêu khoảng, mỗi khoảng là 1 đơn vị.
Ta thấy điểm \( - 4\) cách điểm \(3\) bảy đơn vị.
Cho \(E = \left\{ {3;\, - 8;\,0} \right\}\) . Tập hợp F gồm các phần tử của E và các số đối của chúng là?
-
A.
\(F = \left\{ {3;\,8;\;\,0;\, - 3} \right\}\)
-
B.
\(F = \left\{ { - 3;\, - 8;\,\;0} \right\}\)
-
C.
\(F = \left\{ {3;\, - 8;\,\;0;\, - 3} \right\}\;\)
-
D.
\(F = \left\{ {3;\, - 8;\,\;0;\, - 3;\,\;8} \right\}\)
Đáp án : D
Sử dụng khái niệm tập hợp và khái niệm số đối của tập hợp để tìm ra tập hợp F.
Số đối của a là –a; số đối của 0 là 0.
Tập hợp F gồm các phần tử của E và \(E = \left\{ {3; - \,8;\,0} \right\}\) nên $3; - 8;0$ là các phần tử của tập F
Số đối của 3 là -3
Số đối của -8 là 8
Số đối của 0 là 0
Do đó tập hợp F gồm các phần tử của E và các số đối của chúng là \(F = \left\{ {3;\, - 8;\;\,0;\, - 3;\;\,8} \right\}\)
\(\overline {a001} \left( {a \ne 0} \right)\) bằng
-
A.
\(\overline {a001} = a \times 1000 + 0 \times 100 + 0 \times 10 + 1\)
-
B.
\(\overline {a001} = 1000 + 0 \times 100 + 0 \times 10 + 1\)
-
C.
\(\overline {a001} = a \times 1000 + 1 \times 100\)
-
D.
\(\overline {a001} = a + 0 + 0 + 1\)
Đáp án : A
- Xác định hàng của từng chữ số trong mỗi số.
- Chữ số hàng đơn vị ta giữ nguyên
- Chữ số hàng chục nhân với 10.
- Chữ số hàng trăm nhân với 100.
- Chữ số hàng nghìn nhân với 1000.
Số a là chữ số hàng nghìn nên ta nhân với 1000.
Hai số 0 lần lượt là hàng trăm (nhân với 100) và hàng chục (nhân với 10).
Số 1 là chữ số hàng đơn vị (nhân với 1).
\(\overline {a001} = a \times 1000 + 0 \times 100 + 0 \times 10 + 1\).
Số nào trong các số sau không là số nguyên tố?
-
A.
2
-
B.
3
-
C.
5
-
D.
9
Đáp án : D
- Tìm các ước của 2;3;5;9.
- Số nguyên tố là số tự nhiên lớn hơn \(1,\) chỉ có \(2\) ước là \(1\) và chính nó.
- Chọn số có nhiều hơn 2 ước.
9 chia hết cho 3 nên 3 là một ước của 9. Mà 3 khác 1 và khác 9 nên 9 không là số nguyên tố.
Vậy 9 là số cần tìm.
Số tự nhiên \(m\) nào dưới đây thỏa mãn \({20^{2018}} < {20^m} < {20^{2020}}?\)
-
A.
\(m = 2020\)
-
B.
\(m = 2018\)
-
C.
\(m = 2019\)
-
D.
\(m = 20\)
Đáp án : C
+ So sánh các lũy thừa cùng cơ số : Nếu \({a^m} > {a^n}\) thì \(m > n.\)
+ Từ đó chọn ra các giá trị thích hợp của \(m.\)
Ta có \({20^{2018}} < {20^m} < {20^{2020}}\) suy ra \(2018 < m < 2020\) nên \(m = 2019.\)
Trong một cuộc thi có \(20\) câu hỏi. Mỗi câu trả lời đúng được \(10\) điểm, mỗi câu trả lời sai bị trừ \(3\) điểm. Một học sinh đạt được \(148\) điểm. Hỏi bạn đã trả lời đúng bao nhiêu câu hỏi?
-
A.
$16$
-
B.
$15$
-
C.
$4$
-
D.
$10$
Đáp án : A
Tính tổng số điểm đạt được nếu trả lời đúng hết.
Tính số điểm dư ra so với số điểm đạt được.
Từ đó suy ra số câu trả lời đúng và số câu trả lời sai.
Giả sử bạn học sinh đó trả lời đúng cả \(20\) câu thì tổng số điểm đạt được là \(10.20 = 200\) (điểm)
Số điểm dư ra là \(200 - 148 = 52\) (điểm)
Thay mỗi câu trả lời sai thành câu trả lời đúng thì dư ra \(10 + 3 = 13\) (điểm)
Số câu trả lời sai là \(52:13 = 4\) (câu)
Số câu trả lời đúng \(20 - 4 = 16\) (câu)
Chọn câu sai.
-
A.
Tổng ba số tự nhiên liên tiếp chia hết cho \(3\)
-
B.
Tổng bốn số tự nhiên liên tiếp không chia hết cho \(4\)
-
C.
Tổng năm số tự nhiên chẵn liên tiếp chia hết cho \(10\)
-
D.
Tổng bốn số tự nhiên liên tiếp chia hết cho \(4\)
Đáp án : D
Sử dụng tính chất 1: “Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó” và tính chất 2: “Nếu chỉ có một số hạng của tổng không chia hết cho một số, còn các số hạng khác đều chia hết cho số đó thì tổng không chia hết cho số đó” để giải bài toán.
+) Gọi ba số tự nhiên liên tiếp là \(n;n + 1;n + 2\) $\left( {n \in N} \right)$ thì tổng ba số tự nhiên liên tiếp là \(n + n + 1 + n + 2 = 3n + 3\). Vì \(3 \vdots 3\) nên \(\left( {3n + 3} \right) \vdots 3\) suy ra A đúng.
+) Gọi bốn số tự nhiên liên tiếp là \(n;n + 1;n + 2;n + 3\) $\left( {n \in N} \right)$ thì tổng bốn số tự nhiên liên tiếp là \(n + n + 1 + n + 2 + n + 4 = 4n + 7\). Vì $4 \vdots 3;\,7\not \vdots \,4$ nên \(\left( {4n + 7} \right)\not \vdots 4\) suy ra B đúng, D sai.
+) Gọi năm số tự nhiên chẵn liên tiếp là \(2n;2n + 2;2n + 4;2n + 6;2n + 8\) $\left( {n \in N} \right)$ thì tổng năm số tự nhiên chẵn liên tiếp là \(2n + 2n + 2 + 2n + 4 + 2n + 6 + 2n + 8 = 10n + 20\). Vì $10 \vdots 10;\,20 \vdots 10$ nên \(\left( {10n + 20} \right) \vdots 10\) suy ra C đúng.
Cho số \(A = \overline {a785b} \) . Tìm tổng các chữ số $a$ và $b$ sao cho $A$ chia $9$ dư $2.$
-
A.
\(\left( {a + b} \right) \in \left\{ {9;18} \right\}\)
-
B.
\(\left( {a + b} \right)\in \left\{ {0;9;18} \right\}\)
-
C.
\(\left( {a + b} \right) \in \left\{ {1;2;3} \right\}\)
-
D.
\(\left( {a + b} \right)\in \left\{ {4;5;6} \right\}\)
Đáp án : A
Áp dụng: Một số chia $9$ dư bao nhiêu thì tổng các chữ số của nó chia $9$ cũng dư bấy nhiêu.
Ta có: \(a;\,\,b\,\,\, \in \left\{ {0;\,\,1;\,\,2;\,\,3;\,\,4;\,\,5;\,\,6;\,\,7;\,\,8;\,\,9} \right\}\) và \(a \ne 0.\)
A chia $9$ dư $2$ \( \Rightarrow a + 7 + 8 + 5 + b = a + b + 20\) chia $9$ dư $2$ hay \(\left( {a + b + 18} \right)\,\, \vdots \,\,9\) .
Mà \(18 \, \vdots \, 9 \Rightarrow \left( {a + b} \right) \, \vdots \, 9 \Rightarrow \left( {a + b} \right) \in \left\{ {9;18} \right\}\).
Một căn phòng hình chữ nhật dài $680$cm, rộng $480$cm. Người ta muốn lát kín căn phòng đó bằng gạch hình vuông mà không có viên gạch nào bị cắt xén. Hỏi viên gạch có độ dài lớn nhất là bao nhiêu?
-
A.
$5\,cm$
-
B.
$10\,cm$
-
C.
$20\,cm$
-
D.
$40\,cm$
Đáp án : D
Vì muốn lát gạch kín căn phòng mà không có viên gạch nào bị cắt xén thì độ dài cạnh viên gạch phải là ước của $680$ và $480.$ Để viên gạch có độ dài lớn nhất thì đồ dài cạnh viên gạch bằng ƯCLN$\left( {680;480} \right).$
Ta có: Gọi chiều dài viên gạch là $x.$ Để lát kín căn phòng mà không có có viên gạch nào bị cắt xén thì $x$ phải là ước của chiều dài và chiều rộng căn phòng Hay $680 \, \vdots \, x$ và $480 \, \vdots \, x$ $ \Rightarrow x \in $ ƯC$\left( {680;480} \right)$ Để x là lớn nhất $ \Rightarrow x = $ƯCLN$\left( {680;480} \right)$ Ta có: $680 = {2^3}.5.17;$ $480 = {2^5}.3.5$ $ \Rightarrow x = $ ƯCLN$\left( {680;480} \right)$$ = {2^3}.5 = 40$ Vậy để lát kín căn phòng mà không có viên gạch nào bị cắt xén thì độ dài cạnh viên gạch lớn nhất là $40$ $cm.$
-
A.
\( - 2021;\,\, - 10;\,\,4;\,0;\, - 1\)
-
B.
\( - 2021;\,\, - 10;\,\, - 1;\,\,0;\,\,4\)
-
C.
\( - 2021;\,\, - 10;\,\,0;\,\, - 1;\,\,4\)
-
D.
\(4;\,0;\, - 1;\, - 10;\, - 2021\)
Đáp án : B
- So sánh các số
- Sắp xếp các số nguyên theo thứ tự tăng dần tức là số nào nhỏ hơn ta viết trước, số lớn hơn ta viết sau.
Ta có: \( - 2021 < \, - 10 < \, - 1 < \,\,0 < \,\,4\).
Sắp xếp theo thứ tự tăng dần: \( - 2021;\,\, - 10;\,\, - 1;\,\,0;\,\,4\)
Tổng các số nguyên âm nhỏ nhất có $3$ chữ số và số nguyên âm lớn nhất có $3$ chữ số là:
-
A.
\( - 1099\)
-
B.
\(1099\)
-
C.
\( - 1009\)
-
D.
\( - 1199\)
Đáp án : A
Bước 1: Tìm các số nguyên âm lớn nhất có 3 chữ số và số nguyên âm nhỏ nhất có 3 chữ số Bước 2: Tính tổng các số vừa tìm được ở bước 1
Ta có số nguyên âm lớn nhất có ba chữ số là \( - 100.\)
Số nguyên âm nhỏ nhất có ba chữ số là \( - 999.\)
Nên tổng cần tìm là \(\left( { - 100} \right) + \left( { - 999} \right) = - \left( {100 + 999} \right) = - 1099.\)
Cho \(A = \left( {135 - 35} \right).\left( { - 47} \right) + 53.\left( { - 48 - 52} \right)\) và \(B = 25.\left( {75 - 49} \right) + 75.\left| {25 - 49} \right|.\)
Chọn câu đúng.
-
A.
\(A\) và \(B\) đối nhau
-
B.
\(A\) và \(B\) bằng nhau
-
C.
\(A\) và \(B\) cùng dấu
-
D.
\(A\) và \(B\) trái dấu
Đáp án : D
+) Thực hiện phép tính trong ngoặc trước, đổi dấu hai thừa số, đặt thừa số chung rồi áp dụng quy tắc nhân hai số nguyên khác dấu.
+) Lập luận để phá dấu giá trị tuyệt đối, áp dụng tính chất phân phối để nhân phá ngoặc, nhóm các tích và đặt thừa số chung, sử dụng quy tắc nhân hai số nguyên cùng dấu.
\(\begin{array}{l}A = \left( {135 - 35} \right).\left( { - 47} \right) + 53.\left( { - 48 - 52} \right)\\ = 100.\left( { - 47} \right) + 53.\left( { - 100} \right)\\ = \left( { - 100} \right).47 + 53.\left( { - 100} \right)\\ = \left( { - 100} \right).\left( {47 + 53} \right)\\ = \left( { - 100} \right).100\\ = - 10000\end{array}\)
Vì \(25 - 49 < 0\) nên \(\left| {25 - 49} \right| = - \left( {25 - 49} \right) = 49 - 25\)
\(\begin{array}{l}B = 25.\left( {75 - 49} \right) + 75.\left| {25 - 49} \right|\\ = 25.\left( {75 - 49} \right) + 75.\left( {49 - 25} \right)\\ = 25.75 - 25.49 + 75.49 - 75.25\\ = \left( {25.75 - 75.25} \right) + \left( { - 25.49 + 75.49} \right)\\ = 0 + 49.\left( { - 25 + 75} \right)\\ = 49.50\\ = 2450\end{array}\)
Do đó \(A\) và \(B\) là hai số nguyên trái dấu.
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều

-
A.
8
-
B.
2
-
C.
4
-
D.
6
Đáp án : D
Đếm số tam giác đều đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
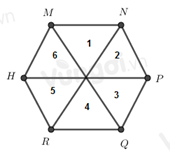
Ta đánh số như hình trên
Nhận thấy có các hình tam giác đều là: 1, 2, 3, 4, 5, 6.
Vậy có 6 tam giác đều.

Cho chu vi tứ giác ACDE bằng 45 cm, chu vi tam giác ABC bằng 32 cm, AC = 10 cm. Khi đó chu vi hình ABCDE là:
-
A.
77 cm
-
B.
67 cm
-
C.
57 cm
-
D.
87 cm
Đáp án : C
- Tính tổng chu vi tứ giác ACDE và tam giác ABC.
- Chu vi hình ABCDE = tổng - 2.AC
Tổng chu vi tứ giác ACDE và tam giác ABC là:
\(45 + 32 = 77\) (cm)
Trong tổng trên cạnh AC đã được tính hai lần, mà hình ABCDE không chứa cạnh AC nên:
Chu vi hình ABCDE là: \(77 - 2.10 = 57\) (cm)
Biểu đồ tranh dưới đây cho biết số học sinh nữ của các lớp khối 6 trường THCS Hoàng Việt.

Em hãy quan sát biểu đồ tranh ở trên và chọn đáp án đúng
-
A.
Lớp 6A1 có ít học sinh nữ nhất
-
B.
Lớp 6A4 có nhiều học sinh nữ hơn lớp 6A5
-
C.
Lớp 6A6 có 20 học sinh nữ.
-
D.
Tổng số học sinh nữ của các lớp khối 6 là 120 học sinh
Đáp án : C
Đếm số biểu tượng để tính số HS nữ của mỗi lớp (mỗi biểu tượng ứng với 10 HS nữ).
Số học sinh nữ.
Lớp 6A1: 2.10 = 20 học sinh nữ
Lớp 6A2: 3.10 = 30 học sinh nữ
Lớp 6A3: 1.10 = 10 học sinh nữ
Lớp 6A4: 2.10 = 20 học sinh nữ
Lớp 6A5: 3.10 = 30 học sinh nữ
Lớp 6A6: 2.10 = 20 học sinh nữ
Lớp 6A3 có ít học sinh nữ nhất (10 học sinh) => A sai
Lớp 6A5 có 30 học sinh nữ, lớp 6A4 có 20 học sinh nữ => Lớp 6A4 có ít học sinh nữ
hơn lớp 6A5. => B sai.
Lớp 6A6 có 20 học sinh nữ. => C đúng.
Tổng số học sinh nữ của các lớp khối 6 là: 20 + 30 + 10 + 20 + 30 + 20 = 130 học sinh.
=> D sai.
Tìm số \(\overline {xy} \) biết \(\overline {xy} .\overline {xyx} = \overline {xyxy} \)
-
A.
\(10\)
-
B.
\(11\)
-
C.
\(12\)
-
D.
\(13\)
Đáp án : A
Sử dụng mối quan hệ giữa các hàng trăm, hàng chục hàng đơn vị khi phân tích một số trong hệ thập phân
Ta có \(\overline {xy} .\overline {xyx} = \overline {xyxy} \)
\(\overline {xy} .\overline {xyx} = \overline {xy} .100 + \overline {xy} \)
\(\overline {xy} .\overline {xyx} = \overline {xy} \left( {100 + 1} \right)\)
\(\overline {xy} .\overline {xyx} = \overline {xy} .101\)
Suy ra \(\overline {xyx} = 101\) nên \(x = 1;y = 0\)
Vậy \(\overline {xy} = 10.\)
Cho \(C = 1 + 3 + {3^2} + {3^3} + ... + {3^{11}}\) . Khi đó \(C\) chia hết cho số nào dưới đây?
-
A.
\(9\)
-
B.
\(11\)
-
C.
\(13\)
-
D.
\(12\)
Đáp án : C
Tổng C có 12 số hạng nên nhóm ba số hạng liền nhau , biến đổi để chứng minh dựa vào tính chất : \(a \, \vdots \, m \Rightarrow a.k \, \vdots \, m \, (k \in \mathbb{N})\)
Ghép ba số hạng liên tiếp thành một nhóm , ta được
\(C = 1 + 3 + {3^2} + {3^3} + ... + {3^{11}}\)\( = \left( {1 + 3 + {3^2}} \right) + \left( {{3^3} + {3^4} + {3^5}} \right)... + \left( {{3^9} + {3^{10}} + {3^{11}}} \right)\)
\( = \left( {1 + 3 + {3^2}} \right) + {3^3}\left( {1 + 3 + {3^2}} \right) + ... + {3^9}\left( {1 + 3 + {3^2}} \right)\)\( = \left( {1 + 3 + {3^2}} \right)\left( {1 + {3^3} + {3^6} + {3^9}} \right)\)
\( = 13.\left( {1 + {3^3} + {3^6} + {3^9}} \right) \, \vdots \, 13\) (do \(13 \, \vdots \, 13\))
Vậy \(C \, \vdots \, 13.\)
Cho hình bình hành có chu vi là 480cm, có độ dài cạnh đáy gấp 5 lần cạnh kia và gấp 8 lần chiều cao. Tính diện tích hình bình hành
-
A.
5000 cm
-
B.
10000 cm
-
C.
2500 cm 2
-
D.
5000 cm 2
Đáp án : D
- Tính nửa chu vi hình bình hành
- Tính cạnh đáy của hình bình hành
- Tính chiều cao của hình bình hành
=> Diện tích hình bình hành
Diện tích hình bình hành là: \(S = b.h\)
Trong đó \(b\) là cạnh, \(h\) là chiều cao tương ứng.
- Ta có nửa chu vi hình bình hành là: 480 : 2 = 240 (cm)
Cạnh đáy gấp 5 lần cạnh kia nên nửa chu vi sẽ gấp 6 lần cạnh kia.
- Ta có cạnh đáy hình bình hành là: 240 : 6 . 5 = 200 (cm)
- Chiều cao của hình bình hành là: 200 : 8 = 25 (cm)
- Diện tích của hình bình hành là: 200 . 25 = 5000 (cm 2 )
Tìm các giá trị thích hợp của chữ số $a$ sao cho: \( - \overline {a99} > - 649 > - \overline {6a0} \)
-
A.
$6$
-
B.
$5$
-
C.
$4$
-
D.
$7$
Đáp án : B
Dựa vào việc so sánh hai số nguyên:
+ Với \(a,b \in Z\), nếu điểm $a$ nằm bên trái điểm $b$ trên trục số nằm ngang thì \(a < b\)
+ Số nguyên $b$ là số liền sau của số nguyên $a$ nếu \(a < b\) và giữa $a$ và $b$ không có số nguyên nào nữa.
\( - \overline {a99} > - 649 > - \overline {6a0} \Rightarrow \overline {a99} < 649 < \overline {6a0} \Rightarrow \left\{ \begin{array}{l}a < 6\\4 < a\end{array} \right. \Rightarrow 4 < a < 6\).
Mà \(a \in {N^*}\) nên \(a = 5\).