Giải bài 1.1 trang 8 sách bài tập toán 12 - Kết nối tri thức
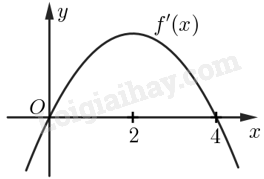
Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\) và đạo hàm \(f'\left( x \right)\) có đồ thị như hình bên. Sử dụng đồ thị của hàm số \(y = f'\left( x \right)\), hãy cho biết: a) Các khoảng đồng biến, khoảng nghịch biến của hàm số \(f\left( x \right)\); b) Hàm số \(f\left( x \right)\) có cực đại, cực tiểu không? Nếu có, hãy cho biết các điểm cực trị tương ứng.
Đề bài
Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\) và đạo hàm \(f'\left( x \right)\) có đồ thị như hình bên. Sử dụng đồ thị của hàm số \(y = f'\left( x \right)\), hãy cho biết:
a) Các khoảng đồng biến, khoảng nghịch biến của hàm số \(f\left( x \right)\);
b) Hàm số \(f\left( x \right)\) có cực đại, cực tiểu không? Nếu có, hãy cho biết các điểm cực trị tương ứng.
Phương pháp giải - Xem chi tiết
Ý a: Quan sát đồ thị để xác định dấu của đạo hàm, từ đó biết được các khoảng đồng biến, nghịch biến của hàm số.
Ý b: Xác định các điểm trên đồ thị mà tại đó đạo hàm đổi dấu, đó chính là các điểm cực trị của hàm số.
Lời giải chi tiết
a) Từ đồ thị ta có:
\(f'\left( x \right) > 0{\rm{ }}\forall {\rm{x}} \in \left( {0;4} \right)\) nên hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( {0;4} \right)\).
\(f'\left( x \right) < 0{\rm{ }}\)với mọi \({\rm{x}}\) thuộc \(\left( { - \infty ;0} \right)\) và \({\rm{x}}\) thuộc \(\left( {4; + \infty } \right)\) nên hàm số \(f\left( x \right)\) nghịch biến trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {4; + \infty } \right)\).
b) Ta có hàm số \(f\left( x \right)\) liên tục và có đạo hàm trên \(\mathbb{R}\). Vì \(f'\left( x \right)\) đổi dấu từ âm sang dương khi \(x\) đi qua \(0\) nên hàm số \(f\left( x \right)\) đạt cực tiểu tại \(x = 0\); \(f'\left( x \right)\) đổi dấu từ dương sang âm khi \(x\) đi qua \(4\) nên hàm số \(f\left( x \right)\) đạt cực đại tại \(x = 4\)