Giải bài 1. 2 trang 9 sách bài tập toán 12 - Kết nối tri thức — Không quảng cáo

Đề bài

Tìm các khoảng đồng biến, khoảng nghịch biến và cực trị (nếu có) của các hàm số sau:

a) $y = {x^3} - 9{x^2} - 48x + 52$;

b) $y =  - {x^3} + 6{x^2} + 9$.

Lời giải chi tiết

a) Tập xác định: $\mathbb{R}$

Ta có $y' = 3{x^2} - 18x - 48$. Khi đó $y' = 0 \Leftrightarrow 3{x^2} - 18x - 48 = 0 \Leftrightarrow x =  - 2$ hoặc $x = 8$.

Lập bảng biến thiên của hàm số:

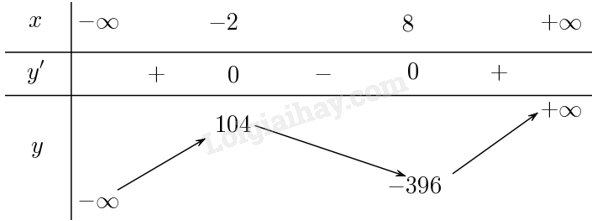
Từ bảng biến thiên, ta có:

Hàm số đồng biến trên các khoảng $\left( { - \infty ; - 2} \right)$ và $\left( {8; + \infty } \right)$, hàm số nghịch biến trên khoảng $\left( { - 2;8} \right)$.

Hàm số đạt cực đại tại $x =  - 2$ và ${y_{CĐ}} = y\left( -2 \right) = 104$.

Hàm số đạt cực tiểu tại $x = 8$ và ${y_{CT}} = y\left( 8 \right) =  - 396$.

b) Tập xác định: $\mathbb{R}$

Ta có $y' =  - 3{x^2} + 12x$. Khi đó $y' = 0 \Leftrightarrow  - 3{x^2} + 12x = 0 \Leftrightarrow x = 0$ hoặc $x = 4$.

Lập bảng biến thiên của hàm số:

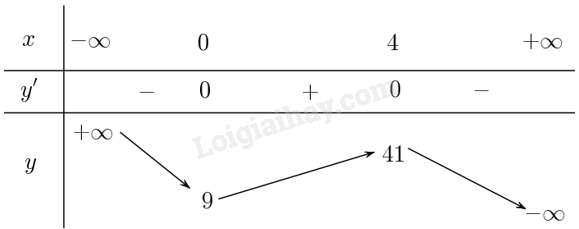
Từ bảng biến thiên, ta có:

Hàm số đồng biến trên khoảng $\left( {0;4} \right)$, hàm số nghịch biến trên các khoảng $\left( { - \infty ;0} \right)$ và

$\left( {4; + \infty } \right)$.

Hàm số đạt cực đại tại $x = 4$ và ${y_{CĐ}} = y\left( 4 \right) = 41$.

Hàm số đạt cực tiểu tại $x = 0$ và ${y_{CT}} = y\left( 0 \right) = 9$.