Giải bài 10 trang 9 sách bài tập toán 11 - Chân trời sáng tạo tập 1
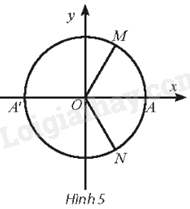
Trong hình bên, các điểm M, A’, N tạo thành ba đỉnh của một tam giác đều. Vị trí các điểm M, A’, N trên đường tròn lượng giác có thể được biểu diễn cho góc lượng giác nào sau đây?
Đề bài
Trong hình bên, các điểm M, A’, N tạo thành ba đỉnh của một tam giác đều. Vị trí các điểm M, A’, N trên đường tròn lượng giác có thể được biểu diễn cho góc lượng giác nào sau đây?
\(\frac{\pi }{3} + k\frac{{2\pi }}{3}\left( {k \in \mathbb{Z}} \right); - \pi + k\frac{{2\pi }}{3}\left( {k \in \mathbb{Z}} \right); - \frac{\pi }{3} + k\frac{\pi }{3}\left( {k \in \mathbb{Z}} \right)\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về biểu diễn góc lượng giác trên đường tròn lượng giác.
Lời giải chi tiết
+) Xét góc lượng giác \(\frac{\pi }{3} + k\frac{{2\pi }}{3}\left( {k \in \mathbb{Z}} \right)\):
Với \(k = 0\) thì ta có góc lượng giác \(\alpha = \frac{\pi }{3}\) biểu diễn là điểm M trên đường tròn lượng giác.
Với \(k = - 1\) thì ta có góc lượng giác \(\beta = - \frac{\pi }{3}\) biểu diễn là điểm N trên đường tròn lượng giác.
Với \(k = 1\) thì ta có góc lượng giác \(\gamma = \pi \) biểu diễn là điểm A’ trên đường tròn lượng giác.
Do đó, vị trí các điểm M, A’, N trên đường tròn lượng giác có thể biểu diễn cho góc lượng giác \(\frac{\pi }{3} + k\frac{{2\pi }}{3}\left( {k \in \mathbb{Z}} \right)\).
+) Xét góc lượng giác \( - \pi + k\frac{{2\pi }}{3}\left( {k \in \mathbb{Z}} \right)\):
Với \(k = 0\) thì ta có góc lượng giác \(\alpha = - \pi \) biểu diễn là điểm A’ trên đường tròn lượng giác
Với \(k = 1\) thì ta có góc lượng giác \(\beta = - \frac{\pi }{3}\) biểu diễn là điểm N trên đường tròn lượng giác
Với \(k = 2\) thì ta có góc lượng giác \(\gamma = \frac{\pi }{3}\) biểu diễn là điểm M trên đường tròn lượng giác
Do đó, vị trí các điểm M, A’, N trên đường tròn lượng giác có thể biểu diễn cho góc lượng giác \( - \pi + k\frac{{2\pi }}{3}\left( {k \in \mathbb{Z}} \right)\).
+) Xét góc lượng giác \( - \frac{\pi }{3} + k\frac{\pi }{3}\left( {k \in \mathbb{Z}} \right)\):
Với \(k = 1\) ta có góc lượng giác bằng 0, được biểu diễn bởi điểm A, không thỏa mãn yêu cầu bài toán.