Giải bài 27 trang 17 sách bài tập toán 12 - Cánh diều — Không quảng cáo

Đề bài

Giá trị lớn nhất của hàm số $y = \frac{{2{\rm{x}} - 1}}{{x - 2}}$ trên nửa khoảng $\left[ { - 3;2} \right)$ bằng:

A. $- \frac{7}{5}$.

B. 7.

C. $\frac{7}{5}$.

D. ‒7.

Lời giải chi tiết

Xét hàm số $y = \frac{{2{\rm{x}} - 1}}{{x - 2}}$ trên nửa khoảng $\left[ { - 3;2} \right)$.

Ta có:

${y^\prime } = \frac{{ - 3}}{{{{\left( {x - 2} \right)}^2}}} < 0,\forall x \ne 2$

Bảng biến thiên của hàm số:

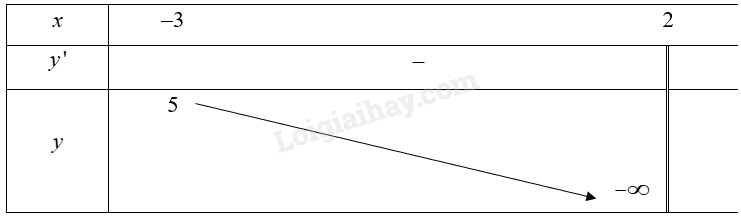
Căn cứ vào bảng biến thiên, ta có: $\mathop {\max }\limits_{\left[ { - 3;2} \right)} f\left( x \right) = \frac{7}{5}$ tại ${\rm{x}} =  - 3$.

Chọn C.