Giải bài 39 trang 16 sách bài tập toán 10 - Cánh diều — Không quảng cáo

Đề bài

Cho $A = \left( { - \infty ;m + 1} \right),B = \left[ {3; + \infty } \right)$ với m là một tham số thực. Tìm m để:

a) $A \cup B = \mathbb{R}$

b) $A \cap B$chứa đúng 5 số nguyên

Lời giải chi tiết

a) Trường hợp 1: $3 < m + 1$

=> $A \cup B = \mathbb{R}$

Tường hợp 2: $m + 1 < 3$

=> $A \cup B = \mathbb{R} \backslash  [m+1;3)$

Trường hợp 3: $m + 1 = 3$

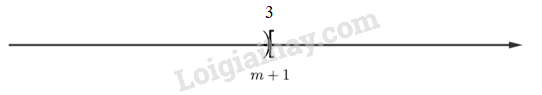
=> $A \cup B = \mathbb{R}$

Để $A \cup B = \mathbb{R}$ thì $m + 1 \ge 3 \Leftrightarrow m \ge 2$

Vậy với $m \ge 2$ thì $A \cup B = \mathbb{R}$

b) Ta có: $A \cap B = \{ x \in \mathbb{R}|x < m + 1$ và $x \ge 3\}  = \{ x \in \mathbb{R}|3 \le x < m + 1\}$

Để $A \cap B \ne \emptyset$thì $m + 1 \ge 3 \Leftrightarrow m \ge 2\quad (1)$

Khi đó $A \cap B = \left[ {3;m + 1} \right)$

Để tập hợp $A \cap B$ chưa đúng 5 số nguyên thì $A \cap B = \left\{ {3;4;5;6;7} \right\}$ tức là $7 < m + 1 \le 8$(2)

Kết hợp (1) và (2) ta được $6 < m \le 7$

Vậy với $6 < m \le 7$thì$A \cap B$ chứa đúng 5 số nguyên