Giải bài 5 trang 63 sách bài tập toán 12 - Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho hình lập phương $ABCD.A'B'C'D'$. Gọi $O,O'$lần lượt là tâm của các hình vuông $ABCD$ và $A'B'C'D'$; $I$ là giao điểm của $AC'$ và $A'C$. Chứng minh rằng:

a) $\overrightarrow {OA'}  + \overrightarrow {OB'}  + \overrightarrow {OC'}  + \overrightarrow {OD'}  = 4\overrightarrow {OO'}$;

b) $\overrightarrow {DB}  + \overrightarrow {DD'}  = 2\overrightarrow {DI}$.

Lời giải chi tiết

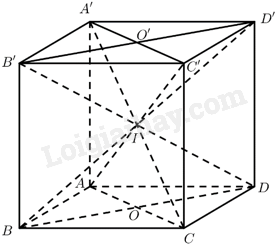
a) $\overrightarrow {OA'}  + \overrightarrow {OB'}  + \overrightarrow {OC'}  + \overrightarrow {OD'}  = \left( {\overrightarrow {OA'}  + \overrightarrow {OC'} } \right) + \left( {\overrightarrow {OB'}  + \overrightarrow {OD'} } \right) = 2\overrightarrow {OO'}  + 2\overrightarrow {OO'}  = 4\overrightarrow {OO'}$

b) Ta có: $A'B'\parallel C{\rm{D}},A'B' = C{\rm{D}}$

Suy ra $A'B'C{\rm{D}}$ là hình bình hành.

Do đó $A'C$ và $B'D$ cắt nhau tại trung điểm mỗi đường.

Vì $I$ là trung điểm của $A'C$ nên $I$ là trung điểm của $B'D$.

Suy ra $\overrightarrow {DB}  + \overrightarrow {DD'}  = \overrightarrow {DB'}  = 2\overrightarrow {DI}$.