Trắc nghiệm Bài 13: Hình chữ nhật Toán 8 Kết nối tri thức
Đề bài
Điền từ, cụm từ thích hợp vào chỗ (…) trong câu sau để được khẳng định đúng:
“ Tứ giác có ... là hình chữ nhật.”
-
A.
hai góc vuông.
-
B.
bốn góc vuông.
-
C.
bốn cạnh bằng nhau.
-
D.
các cạnh đối song song.
Hai đường chéo của hình chữ nhật có tính chất nào sau đây?
-
A.
Chúng vuông góc với nhau.
-
B.
Chúng bằng nhau.
-
C.
Chúng cắt nhau tại trung điểm của mỗi đường.
-
D.
Chúng bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Chọn khẳng định đúng trong các khẳng định sau
-
A.
Hình chữ nhật là tứ giác có bốn cạnh bằng nhau.
-
B.
Hình chữ nhật là tứ giác có bốn góc vuông.
-
C.
Hình chữ nhật là tứ giác có hai góc vuông.
-
D.
Hình chữ nhật là tứ giác có hai đường chéo bằng nhau.
Hình chữ nhật có mấy tâm đối xứng?
-
A.
1.
-
B.
2.
-
C.
3.
-
D.
4.
Hình bình hành cần có thêm điều kiện nào sau đây thì trở thành hình chữ nhật?
-
A.
Có một góc vuông.
-
B.
Có hai cạnh kề bằng nhau.
-
C.
Có hai đường chéo vuông góc.
-
D.
Có hai đường chéo cắt nhau tại trung điểm mỗi đường.
Hình bình hành \(ABCD\) là hình chữ nhật khi
-
A.
\(AB{\rm{ }} = AD\).
-
B.
\(\widehat A = {90^o}\).
-
C.
\(AB = 2AC\).
-
D.
\(\widehat A = \widehat C\).
Chọn câu sai. Tứ giác ABCD là hình chữ nhật khi:
-
A.
\(\widehat A = \widehat B = \widehat C = {90^o}\)
-
B.
\(\widehat A = \widehat B = \widehat C = {90^o}\) và AB // CD
-
C.
AB = CD = AD = BC
-
D.
AB // CD; AB = CD; AC = BD
Hãy chọn câu đúng. Cho ΔABC với M thuộc cạnh BC. Từ M vẽ ME song song với AB và MF song song với AC. Hãy xác định điều kiện của ΔABC để tứ giác AEMF là hình chữ nhật.
-
A.
ΔABC vuông tại A
-
B.
ΔABC vuông tại B
-
C.
ΔABC vuông tại C
-
D.
ΔABC đều
Cho tam giác ABC vuông tại A, điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là chân đường vuông góc kẻ từ M đến AB, AC. Điểm M ở vị trí nào trên BC thì DE có độ dài nhỏ nhất?
-
A.
M là hình chiếu của A trên BC
-
B.
M là trung điểm của BC
-
C.
M trùng với B
-
D.
Đáp án khác
Cho tam giác \(ABC\), đường cao \(AH\). \(I\) là trung điểm của \(AC\), \(E\) đối xứng với \(H\)qua \(I\). Tứ giác \(AHCE\) là hình gì?
-
A.
Hình thang.
-
B.
Hình thang cân.
-
C.
Hình thang vuông.
-
D.
Hình chữ nhật.
Hình chữ nhật \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Biết \(\widehat {AOD} = {50^o}\), tính số đo \(\widehat {ABO}\).
-
A.
\({50^o}\).
-
B.
\({25^o}\).
-
C.
\({90^o}\).
-
D.
\({130^o}\).
Cho tam giác \(ABC\) vuông tại \(A\). Gọi \(M\), N, \(P\) lần lượt là trung điểm thuộc các cạnh \(AB\), AC, \(BC\) và \(MP = \frac{{AC}}{2}\), \(MP\;{\rm{//}}\;AN\).Tứ giác \(AMPN\) là hình gì?
-
A.
Hình thang.
-
B.
Hình thang cân.
-
C.
Hình chữ nhật.
-
D.
Hình thang vuông.
Cho hình chữ nhật \(ABCD\). \(E\), \(F\), \(G\), \(H\) là trung điểm của các cạnh \(AB\), \(BC\), \(CD\), \(DA\) và \(EF\;\;{\rm{//}}\;\;AC\), \(GH\;\;{\rm{//}}\;\;AC\);\(EH\;\;{\rm{//}}\;\;BD\),\(FG\;\;{\rm{//}}\;\;BD\) Tứ giác \(EFGH\) là hình gì?
-
A.
Hình chữ nhật.
-
B.
Hình thang cân.
-
C.
Hình thang.
-
D.
Hình bình hành.
Cho tam giác ABC vuông cân tại A, AC = 6cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Chu vi của tứ giác ADME bằng:
-
A.
6cm
-
B.
36cm
-
C.
18cm
-
D.
12cm
Cho tam giác ABC với ba trung tuyến AI, BD, CE đồng quy tại G sao cho ED // BC; \(E{\rm{D}} = \frac{1}{2}BC\) . M và N lần lượt là các điểm của GC và GB và MN // BC; \(MN = \frac{1}{2}BC\); Tứ giác MNED là hình gì?
-
A.
Hình chữ nhật
-
B.
Hình bình hành
-
C.
Hình thang cân
-
D.
Hình thang vuông
Cho hình thang vuông \(ABCD\) có \(\widehat A = \widehat D = {90^o}\) . Gọi \(M\) là trung điểm của \(AC\) và \(BM{\rm{ }} = {\rm{ }}\frac{1}{2}AC\) . Khẳng định nào sau đây sai
-
A.
\(AC = BD\).
-
B.
Tứ giác \(ABCD\) là hình chữ nhật.
-
C.
\(M\) là trung điểm của \(BD\).
-
D.
\(AB = AD\).
Cho tứ giác \(ABCD\). \(E\), \(F\), \(G\), \(H\) là trung điểm của các cạnh \(AB\), \(BC\), \(CD\), \(DA\)và \(EF\;\;{\rm{//}}\;\;AC\), \(GH\;\;{\rm{//}}\;\;AC\), \(EH\;\;{\rm{//}}\;\;BD\), \(FG\;\;{\rm{//}}\;\;BD\). Tứ giác \(ABCD\) cần thêm điều kiện nào sau đây để tứ giác \(EFGH\) là hình chữ nhật?
-
A.
\(AC = BD\) .
-
B.
\(AC \bot BD\).
-
C.
\(AB = BC\).
-
D.
\(AB\;{\rm{//}}\;CD\) .
Lời giải và đáp án
Điền từ, cụm từ thích hợp vào chỗ (…) trong câu sau để được khẳng định đúng:
“ Tứ giác có ... là hình chữ nhật.”
-
A.
hai góc vuông.
-
B.
bốn góc vuông.
-
C.
bốn cạnh bằng nhau.
-
D.
các cạnh đối song song.
Đáp án : B
Hai đường chéo của hình chữ nhật có tính chất nào sau đây?
-
A.
Chúng vuông góc với nhau.
-
B.
Chúng bằng nhau.
-
C.
Chúng cắt nhau tại trung điểm của mỗi đường.
-
D.
Chúng bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Đáp án : D
Chọn khẳng định đúng trong các khẳng định sau
-
A.
Hình chữ nhật là tứ giác có bốn cạnh bằng nhau.
-
B.
Hình chữ nhật là tứ giác có bốn góc vuông.
-
C.
Hình chữ nhật là tứ giác có hai góc vuông.
-
D.
Hình chữ nhật là tứ giác có hai đường chéo bằng nhau.
Đáp án : B
Hình chữ nhật có mấy tâm đối xứng?
-
A.
1.
-
B.
2.
-
C.
3.
-
D.
4.
Đáp án : A
Hình bình hành cần có thêm điều kiện nào sau đây thì trở thành hình chữ nhật?
-
A.
Có một góc vuông.
-
B.
Có hai cạnh kề bằng nhau.
-
C.
Có hai đường chéo vuông góc.
-
D.
Có hai đường chéo cắt nhau tại trung điểm mỗi đường.
Đáp án : A
Hình bình hành \(ABCD\) là hình chữ nhật khi
-
A.
\(AB{\rm{ }} = AD\).
-
B.
\(\widehat A = {90^o}\).
-
C.
\(AB = 2AC\).
-
D.
\(\widehat A = \widehat C\).
Đáp án : B
Hình bình hành có một góc vuông là hình chữ nhật.
Chọn câu sai. Tứ giác ABCD là hình chữ nhật khi:
-
A.
\(\widehat A = \widehat B = \widehat C = {90^o}\)
-
B.
\(\widehat A = \widehat B = \widehat C = {90^o}\) và AB // CD
-
C.
AB = CD = AD = BC
-
D.
AB // CD; AB = CD; AC = BD
Đáp án : C
+ Ta thấy AB = CD = AD = BC thì ABCD chỉ có bốn cạnh bằng nhau nên ABCD chưa chắc là hình chữ nhật .
Nếu \(\widehat A = \widehat B = \widehat C = {90^o}\) thì tứ giác ABCD có ba góc vuông nên ABCD là hình chữ nhật (do dấu hiệu tứ giác có 3 góc vuông).
+ Nếu \(\widehat A = \widehat B = \widehat C = {90^o}\) và AB // CD thì tứ giác ABCD có AD // BC; AB // CD nên ABCD là hình bình hành, lại có Â = 90 0 nên ABCD là hình chữ nhật. (do dấu hiệu hình bình hành có một góc vuông)
+ Nếu AB // CD; AB = CD và AC = BD thì ABCD là hình bình hành (do có cặp cạnh đối AB; CD song song và bằng nhau), lại có hai đường chéo bằng nhau AC = BD nên ABCD là hình chữ nhật (do dấu hiệu hình bình hành có hai đường chéo bằng nhau).
Hãy chọn câu đúng. Cho ΔABC với M thuộc cạnh BC. Từ M vẽ ME song song với AB và MF song song với AC. Hãy xác định điều kiện của ΔABC để tứ giác AEMF là hình chữ nhật.
-
A.
ΔABC vuông tại A
-
B.
ΔABC vuông tại B
-
C.
ΔABC vuông tại C
-
D.
ΔABC đều
Đáp án : A
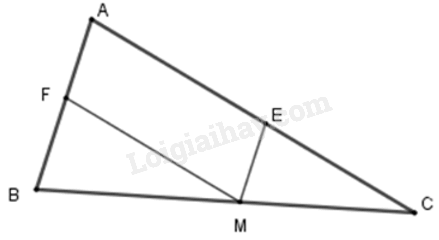
Từ giả thiết ta có ME // AF; MF // AE nên tứ giác AEMF là hình bình hành (dhnb).
Để hình bình hành AEMF là hình chữ nhật thì \(\widehat {{\rm{EAF}}} = {90^o}\) nên tam giác ABC vuông tại A.
Cho tam giác ABC vuông tại A, điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là chân đường vuông góc kẻ từ M đến AB, AC. Điểm M ở vị trí nào trên BC thì DE có độ dài nhỏ nhất?
-
A.
M là hình chiếu của A trên BC
-
B.
M là trung điểm của BC
-
C.
M trùng với B
-
D.
Đáp án khác
Đáp án : C

Xét tứ giác ADME có \(\widehat A = \widehat {A{\rm{D}}M} = \widehat {A{\rm{E}}M} = {90^o}\) nên ADME là hình chữ nhật.
Vì ADME là hình chữ nhật nên AM = DE (tính chất)
Để DE nhỏ nhất thì AM nhỏ nhất mà AM nhỏ nhất khi M là hình chiếu của A trên BC
Từ đó DE nhỏ nhất khi M là hình chiếu của A trên BC.
Cho tam giác \(ABC\), đường cao \(AH\). \(I\) là trung điểm của \(AC\), \(E\) đối xứng với \(H\)qua \(I\). Tứ giác \(AHCE\) là hình gì?
-
A.
Hình thang.
-
B.
Hình thang cân.
-
C.
Hình thang vuông.
-
D.
Hình chữ nhật.
Đáp án : D
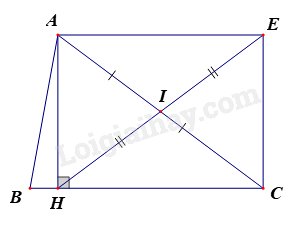
Tứ giác \(AHCE\) là hình bình hành vì \(IA = IC\), \(IH = IE\).
Mà \(\widehat H = {90^o}\)\( \Rightarrow AHCE\) là hình chữ nhật.
Hình bình hành có một góc vuông là hình chữ nhật
Hình chữ nhật \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Biết \(\widehat {AOD} = {50^o}\), tính số đo \(\widehat {ABO}\).
-
A.
\({50^o}\).
-
B.
\({25^o}\).
-
C.
\({90^o}\).
-
D.
\({130^o}\).
Đáp án : B
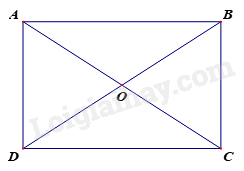
Ta có: \(\widehat {AOB} = {180^o} - \widehat {AOD} = {130^o}\) (hai góc kề bù)
Theo tính chất hình chữ nhật ta có \(OA = OB\) \( \Rightarrow \Delta OAB\) cân tại \(O\)
\( \Rightarrow \widehat {ABO} = \widehat {BAO} = \frac{{{{180}^o} - {{130}^o}}}{2} = {25^o}\).
Cho tam giác \(ABC\) vuông tại \(A\). Gọi \(M\), N, \(P\) lần lượt là trung điểm thuộc các cạnh \(AB\), AC, \(BC\) và \(MP = \frac{{AC}}{2}\), \(MP\;{\rm{//}}\;AN\).Tứ giác \(AMPN\) là hình gì?
-
A.
Hình thang.
-
B.
Hình thang cân.
-
C.
Hình chữ nhật.
-
D.
Hình thang vuông.
Đáp án : C
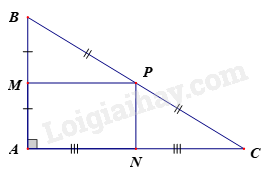
Xét tam giác ABC ta có: \(MP = \frac{{AC}}{2}\), \(MP\;{\rm{//}}\;AN\)
Mà \(AN = \frac{{AC}}{2}\) \( \Rightarrow MP\;{\rm{ = }}\;AN\)
\( \Rightarrow \) Tứ giác \(AMPN\) là hình bình hành
Mà \(\widehat A = {90^o}\)\( \Rightarrow AMPN\) là hình chữ nhật.
Cho hình chữ nhật \(ABCD\). \(E\), \(F\), \(G\), \(H\) là trung điểm của các cạnh \(AB\), \(BC\), \(CD\), \(DA\) và \(EF\;\;{\rm{//}}\;\;AC\), \(GH\;\;{\rm{//}}\;\;AC\);\(EH\;\;{\rm{//}}\;\;BD\),\(FG\;\;{\rm{//}}\;\;BD\) Tứ giác \(EFGH\) là hình gì?
-
A.
Hình chữ nhật.
-
B.
Hình thang cân.
-
C.
Hình thang.
-
D.
Hình bình hành.
Đáp án : D
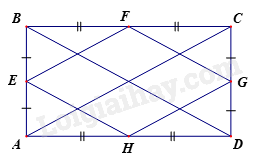
Tứ giác \(EFGH\) là hình bình hành vì
+ \(EF\;\;{\rm{//}}\;\;GH\) (\(EF\;\;{\rm{//}}\;\;AC\), \(GH\;\;{\rm{//}}\;\;AC\))
+ \(EH\;\;{\rm{//}}\;\;FG\) (\(EH\;\;{\rm{//}}\;\;BD\),\(FG\;\;{\rm{//}}\;\;BD\))
Cho tam giác ABC vuông cân tại A, AC = 6cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Chu vi của tứ giác ADME bằng:
-
A.
6cm
-
B.
36cm
-
C.
18cm
-
D.
12cm
Đáp án : D
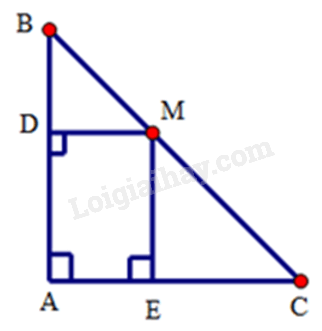
+ Xét tứ giác ADME có \(\widehat A = \widehat B = \widehat C = \widehat D = {90^o}\) nên ADME là hình chữ nhật
+ Xét tam giác DMB có \(\widehat B = {45^o}\) (do tam giác ABC vuông cân) nên tam giác BDM vuông cân tại D. Do đó DM = BD
+ Do ADME là hình chữ nhật nên chu vi ADME là:
(AD + DM).2 = (AD + BD).2 = 6.2 = 12 cm
Vậy chu vi ADME là 12cm
Cho tam giác ABC với ba trung tuyến AI, BD, CE đồng quy tại G sao cho ED // BC; \(E{\rm{D}} = \frac{1}{2}BC\) . M và N lần lượt là các điểm của GC và GB và MN // BC; \(MN = \frac{1}{2}BC\); Tứ giác MNED là hình gì?
-
A.
Hình chữ nhật
-
B.
Hình bình hành
-
C.
Hình thang cân
-
D.
Hình thang vuông
Đáp án : B
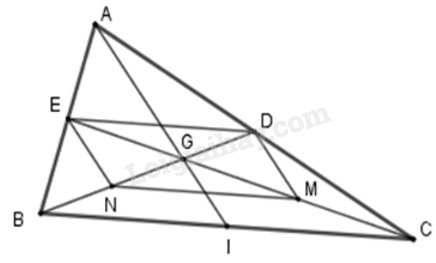
Xét tam giác ABC : ED // BC; \(E{\rm{D}} = \frac{1}{2}BC\) (1)
+ Xét tam giác GBC có : MN // BC; \(MN = \frac{1}{2}BC\) (2)
Từ (1), (2) ⇒ MN // ED, MN = ED nên tứ giác MNED là hình bình hành (dấu hiệu nhận biết)
Cho hình thang vuông \(ABCD\) có \(\widehat A = \widehat D = {90^o}\) . Gọi \(M\) là trung điểm của \(AC\) và \(BM{\rm{ }} = {\rm{ }}\frac{1}{2}AC\) . Khẳng định nào sau đây sai
-
A.
\(AC = BD\).
-
B.
Tứ giác \(ABCD\) là hình chữ nhật.
-
C.
\(M\) là trung điểm của \(BD\).
-
D.
\(AB = AD\).
Đáp án : D
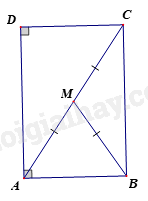
Xét \(\Delta ABC\) có \(BM\) là đường trung tuyến ứng với cạnh \(AC\) mà \(BM{\rm{ }} = {\rm{ }}\frac{1}{2}AC\)\( \Rightarrow \Delta ABC\) vuông tại \(B\)
Tứ giác \(ABCD\) có \(\widehat A = \widehat D = \widehat B = {90^o}\)\( \Rightarrow \) Tứ giác \(ABCD\) là hình chữ nhật.
Suy ra: \(AC = BD\) và \(M\) là trung điểm của \(BD\)
Vậy D sai.
Cho tứ giác \(ABCD\). \(E\), \(F\), \(G\), \(H\) là trung điểm của các cạnh \(AB\), \(BC\), \(CD\), \(DA\)và \(EF\;\;{\rm{//}}\;\;AC\), \(GH\;\;{\rm{//}}\;\;AC\), \(EH\;\;{\rm{//}}\;\;BD\), \(FG\;\;{\rm{//}}\;\;BD\). Tứ giác \(ABCD\) cần thêm điều kiện nào sau đây để tứ giác \(EFGH\) là hình chữ nhật?
-
A.
\(AC = BD\) .
-
B.
\(AC \bot BD\).
-
C.
\(AB = BC\).
-
D.
\(AB\;{\rm{//}}\;CD\) .
Đáp án : B
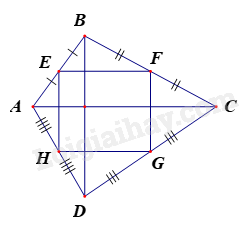
Tứ giác \(EFGH\) là hình bình hành vì
+ \(EF\;\;{\rm{//}}\;\;GH\) (\(EF\;\;{\rm{//}}\;\;AC\), \(GH\;\;{\rm{//}}\;\;AC\))
+ \(EH\;\;{\rm{//}}\;\;FG\) (\(EH\;\;{\rm{//}}\;\;BD\), \(FG\;\;{\rm{//}}\;\;BD\))
Để hình bình hành \(EFGH\) là hình chữ nhật cần thêm điều kiện \(\widehat E = {90^o}\)
\( \Rightarrow EF \bot EH\) \( \Leftrightarrow AC \bot BD\)