Trắc nghiệm Bài 39: Hình chóp tứ giác đều Toán 8 Kết nối tri thức
Đề bài
Đáy của hình chóp tứ đều là hình gì?
-
A.
Hình vuông.
-
B.
Hình thang cân.
-
C.
Hình chữ nhật .
-
D.
Tam giác đều.
Chân đường cao kẻ từ đỉnh của hình chóp tứ giác đều là?
-
A.
trung điểm của cạnh bên.
-
B.
trọng tâm của tam giác đáy.
-
C.
giao điểm hai đường chéo.
-
D.
một điểm bất kì trong mặt phẳng đáy.
Cho hình chóp tứ giác đều có p là nửa chu vi đáy, d là độ dài trung đoạn. Công thức tính diện tích xung quanh của hình chóp tứ giác đều bằng:
-
A.
\({S_{xq}} = \frac{p}{d}\).
-
B.
\({S_{xq}} = \frac{{2p}}{d}\).
-
C.
\({S_{xq}} = p.d\).
-
D.
. \({S_{xq}} = \frac{p}{2}.d\).
Cho hình chóp tứ giác đều, thể tích của hình chóp được tính bằng:
-
A.
\(\frac{1}{3}\) tích của diện tích mặt đáy với chiều cao.
-
B.
\(\frac{1}{3}\) tích của diện tích mặt đáy với trung đoạn.
-
C.
tích của diện tích mặt đáy với chiều cao.
-
D.
tích của diện tích mặt đáy với trung đoạn.
Hình chóp tứ giác đều có mấy mặt?
-
A.
3.
-
B.
4.
-
C.
5.
-
D.
6.
Trung đoạn của hình chóp tứ giác đều là:
-
A.
Đường cao kẻ từ đỉnh tới trọng tâm của mặt đáy.
-
B.
Đường cao kẻ từ đỉnh của mỗi mặt bên.
-
C.
Đường thẳng kẻ từ đỉnh tới trung điểm đường cao cạnh đáy.
-
D.
Đường thẳng kẻ từ đỉnh của hình chóp tới điểm bất kì trong mặt phẳng đáy.
-
A.
HM là trung đoạn của hình chóp tứ giác đều S.ABCD.
-
B.
SH là đường cao của hình chóp tứ giác đều S.ABCD.
-
C.
SM là trung đoạn của hình chóp tứ giác đều S.ABCD.
-
D.
Hình chóp tứ giác đều S.ABCD có mặt bên SAB là tam giác cân.
Cho hình chóp tứ giác đều có nửa chu vi đáy là \(20cm\), độ dài trung đoạn là \(5cm\). Tính diện tích xung quanh của hình chóp đó.
-
A.
\(50c{m^2}\).
-
B.
\(\frac{{100}}{3}c{m^2}\)
-
C.
\(200c{m^2}\).
-
D.
\(100c{m^2}\).
Cho hình chóp tứ giác đều S.ABCD biết SA = a, AB = 2a, chọn phát biểu đúng?
-
A.
\(SD = SA = a\).
-
B.
\(SB = AB = a\).
-
C.
\(SB = BC = 2a\).
-
D.
\(SB = SC = 2a\).
Cho hình chóp tứ giác đều có thể tích là \(50c{m^3}\), chiều cao hình chóp bằng \(5cm\). Tính diện tích mặt đáy của hình chóp đó.
-
A.
\(10c{m^2}\).
-
B.
\(30c{m^2}\)
-
C.
\(50c{m^2}\).
-
D.
\(\frac{{10}}{3}c{m^2}\).
Cho hình chóp tứ giác đều S.ABCD có các mặt bên là các tam giác đều diện tích\(10c{m^2}\). Tính diện tích xung quanh của hình chóp đó.
-
A.
\(10c{m^2}\)
-
B.
\(20c{m^2}\)
-
C.
\(40c{m^2}\)
-
D.
\(30c{m^2}\).
Cho hình chóp tứ giác đều có độ dài cạnh đáy là 3cm, độ dài trung đoạn bằng 5cm. Tính diện tích xung quanh hình chóp.
-
A.
\(10c{m^2}\)
-
B.
\(20c{m^2}\)
-
C.
\(40c{m^2}\)
-
D.
\(30c{m^2}\).
Cho hình chóp tứ giác đều có độ dài trung đoạn d, diện tích xung quanh là S. Chu vi đáy C bằng:
-
A.
\(C = {S_{xq}}.d\)
-
B.
\(C = \frac{{{S_{xq}}}}{{2d}}\)
-
C.
\(C = \frac{{{S_{xq}}}}{d}\)
-
D.
\(C = \frac{{2{S_{xq}}}}{d}\).
Cho khối chóp tứ giác đều, nếu tăng cạnh đáy lên ba lần và giảm chiều cao đi ba lần thì thể tích của khối chóp sẽ:
-
A.
Giảm đi 9 lần.
-
B.
Tăng lên 3 lần.
-
C.
Giảm đi 3 lần.
-
D.
Tăng lên 9 lần.
Chọn phát biểu sai trong các phát biểu sau:
-
A.
Hình chóp tứ giác đều có các mặt bên là tam giác cân.
-
B.
Đường cao của hình chóp tứ giác đều là đoạn thẳng nối đỉnh của hình chóp và trung điểm một cạnh đáy.
-
C.
Đường cao kẻ từ đỉnh của mỗi mặt bên gọi là trung đoạn của hình chóp tứ giác đều.
-
D.
Diện tích xung quanh của hình chóp tứ giác đều bằng tích của nửa chu vi đáy với trung đoạn.
Một hình chóp tứ giác đều có thể tích bằng \(32c{m^3}\), chiều cao hình chóp bằng 6cm, chiều cao mặt bên bằng 10cm. Tính diện tích xung quanh hình chóp đó.
-
A.
\(40(c{m^2})\)
-
B.
\(50(c{m^2})\)
-
C.
\(60(c{m^2})\)
-
D.
\(80(c{m^2})\)
Cho hình chóp tứ giác đều S. ABCD có diện tích xung quanh bằng \(72c{m^2}\) , chiều cao có độ dài bằng 6cm, độ dài trung đoạn băng 4cm. Thể tích của khối chóp đó là?
-
A.
\(36c{m^3}\).
-
B.
\(162c{m^3}\).
-
C.
\(162\sqrt 3 c{m^3}\).
-
D.
\(72c{m^3}\).
Tính diện tích toàn phần của hình chóp tứ giác đều biết cạnh đáy bằng 6cm, độ dài trung đoạn bằng 4cm.
-
A.
\(45c{m^2}\).
-
B.
\(81c{m^2}\).
-
C.
\(36c{m^2}\).
-
D.
\(84c{m^2}\).
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 4cm và chiều cao bằng 5cm. Tính độ dài trung đoạn của hình chóp đó.
-
A.
\(\frac{{\sqrt {17} }}{2}cm\).
-
B.
\(\sqrt {33} cm\).
-
C.
\(\sqrt {29} cm\).
-
D.
\(5cm\).
Cho hình chóp tứ giác đều S. ABCD có chu vi đáy là 20cm, chiều cao có số đo gấp 3 lần cạnh đáy. Thể tích của khối chóp đó là?
-
A.
\(80c{m^3}\).
-
B.
\(125c{m^3}\).
-
C.
\(25c{m^3}\).
-
D.
\(375c{m^3}\).
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau và bằng a. Thể tích V của khối chóp S.ABC.
-
A.
\(\frac{{{a^3}\sqrt 3 }}{2}\).
-
B.
\(\frac{{{a^3}\sqrt 3 }}{6}\).
-
C.
\(\frac{{{a^3}\sqrt 2 }}{6}\).
-
D.
\(\frac{{{a^3}}}{6}\).
Cho mô hình dạng hình chóp tứ giác đều có diện tích bằng \(3600c{m^2}\), trung đoạn của khối gỗ là 80cm. Bạn Nam định sơn 4 mặt khối gỗ đó bằng sơn màu vàng, biết mỗi mét vuông bạn phải trả 50000 đồng tiền sơn. Hỏi bạn Nam sơn hết bao nhiêu tiền?
-
A.
48000 đồng.
-
B.
96000 đồng.
-
C.
24000 đồng.
-
D.
144000 đồng.
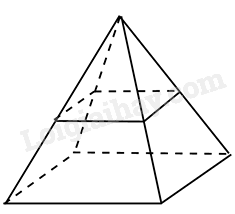
Người ta làm một bugalow dạng hình chóp tứ giác đều có chiều cao 4m, cạnh sàn nhà bằng 6m. Người ta chia đôi làm hai tầng bằng một mặt phẳng song song với sàn, cách đỉnh của hình chóp một khoảng bằng nửa chiều cao, cạnh mặt sàn tầng hai bằng một nửa cạnh mặt sàn tầng một. Biết một người cần \(3{m^3}\)không khí, tính số người tối đa ở tầng dưới. ( hình vẽ dưới)
-
A.
16 người.
-
B.
20 người.
-
C.
18 người.
-
D.
14 người.
Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng a, cạnh bên bằng 2a. Gọi I, H lần lượt là trung điểm cạnh AB, CD. Tính thể tích V của khối chóp S.IBCH.
-
A.
\(V = \frac{{{a^3}\sqrt 2 }}{{12}}\).
-
B.
\(V = \frac{{{a^3}\sqrt 2 }}{6}\).
-
C.
\(V = \frac{{{a^3}\sqrt 2 }}{4}\).
-
D.
\(V = \frac{{{a^3}\sqrt 2 }}{8}\).
Lời giải và đáp án
Đáy của hình chóp tứ đều là hình gì?
-
A.
Hình vuông.
-
B.
Hình thang cân.
-
C.
Hình chữ nhật .
-
D.
Tam giác đều.
Đáp án : A
Sử dụng định nghĩa hình tứ giác đều: Hình chóp tứ giác đều có đáy là hình vuông, các mặt bên là các tam giác cân bằng nhau có chung đỉnh.
Theo định nghĩa hình chóp tứ giác đều, mặt đáy là hình vuông.
Chân đường cao kẻ từ đỉnh của hình chóp tứ giác đều là?
-
A.
trung điểm của cạnh bên.
-
B.
trọng tâm của tam giác đáy.
-
C.
giao điểm hai đường chéo.
-
D.
một điểm bất kì trong mặt phẳng đáy.
Đáp án : C
Sử dụng định nghĩa đường cao của hình chóp tứ giác đều: Chân đường cao kẻ từ đỉnh tới mặt đáy của hình chóp tứ giác đều là điểm cách đều các đỉnh của mặt đáy ( giao điểm hai đường chéo)
Theo định nghĩa: Chân đường cao kẻ từ đỉnh tới mặt đáy của hình chóp tứ giác đều là giao điểm hai đường chéo nên chọn đáp án C
Cho hình chóp tứ giác đều có p là nửa chu vi đáy, d là độ dài trung đoạn. Công thức tính diện tích xung quanh của hình chóp tứ giác đều bằng:
-
A.
\({S_{xq}} = \frac{p}{d}\).
-
B.
\({S_{xq}} = \frac{{2p}}{d}\).
-
C.
\({S_{xq}} = p.d\).
-
D.
. \({S_{xq}} = \frac{p}{2}.d\).
Đáp án : C
Sử dụng công thức tính diện tích xung quanh của hình chóp tứ giác đều
Diện tích xung quanh của hình chóp tứ giác đều bằng tích của nửa chu vi đáy với trung đoạn nên chọn đáp án C
Cho hình chóp tứ giác đều, thể tích của hình chóp được tính bằng:
-
A.
\(\frac{1}{3}\) tích của diện tích mặt đáy với chiều cao.
-
B.
\(\frac{1}{3}\) tích của diện tích mặt đáy với trung đoạn.
-
C.
tích của diện tích mặt đáy với chiều cao.
-
D.
tích của diện tích mặt đáy với trung đoạn.
Đáp án : A
Sử dụng công thức tính thể tích của hình chóp tứ giác đều.
Thể tích của hình chóp tứ giác đều bằng \(\frac{1}{3}\) tích của diện tích đáy với chiều cao của nó nên chọn đáp án A
Hình chóp tứ giác đều có mấy mặt?
-
A.
3.
-
B.
4.
-
C.
5.
-
D.
6.
Đáp án : C
Sử dụng định nghĩa hình chóp tứ giác đều.
Theo định nghĩa hình chóp tứ giác đều thì chọn đáp án C
Trung đoạn của hình chóp tứ giác đều là:
-
A.
Đường cao kẻ từ đỉnh tới trọng tâm của mặt đáy.
-
B.
Đường cao kẻ từ đỉnh của mỗi mặt bên.
-
C.
Đường thẳng kẻ từ đỉnh tới trung điểm đường cao cạnh đáy.
-
D.
Đường thẳng kẻ từ đỉnh của hình chóp tới điểm bất kì trong mặt phẳng đáy.
Đáp án : B
Sử dụng định nghĩa trung đoạn của hình chóp tứ giác đều: Đường cao kẻ từ đỉnh của mỗi mặt bên gọi là trung đoạn của hình chóp tứ giác đều.
Theo định nghĩa trung đoạn của hình chóp tứ giác đều thì chọn đáp án B.
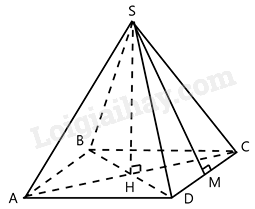
-
A.
HM là trung đoạn của hình chóp tứ giác đều S.ABCD.
-
B.
SH là đường cao của hình chóp tứ giác đều S.ABCD.
-
C.
SM là trung đoạn của hình chóp tứ giác đều S.ABCD.
-
D.
Hình chóp tứ giác đều S.ABCD có mặt bên SAB là tam giác cân.
Đáp án : A
Sử dụng định nghĩa hình chóp tứ giác đều, đường cao, trung đoạn của hình chóp tứ giác đều.
Theo định nghĩa trung đoạn của hình chóp tam giác đều thì trung đoạn của hình chóp S.ABCD là đoạn SH nên A sai
Cho hình chóp tứ giác đều có nửa chu vi đáy là \(20cm\), độ dài trung đoạn là \(5cm\). Tính diện tích xung quanh của hình chóp đó.
-
A.
\(50c{m^2}\).
-
B.
\(\frac{{100}}{3}c{m^2}\)
-
C.
\(200c{m^2}\).
-
D.
\(100c{m^2}\).
Đáp án : D
Sử dụng công thức tính diện tích xung quanh của hình chóp tam giác đều: \({S_{xq}} = p.d\)
Theo công thức tính diện tích xung quanh của hình chóp tam giác đều:
\({S_{xq}} = p.d = 20.5 = 100c{m^2}\)
Cho hình chóp tứ giác đều S.ABCD biết SA = a, AB = 2a, chọn phát biểu đúng?
-
A.
\(SD = SA = a\).
-
B.
\(SB = AB = a\).
-
C.
\(SB = BC = 2a\).
-
D.
\(SB = SC = 2a\).
Đáp án : A
Sử dụng kiến thức về các cạnh của hình chóp tứ giác đều: Hình chóp tứ giác đều có đáy là hình vuông, các mặt bên là các tam giác cân bằng nhau có chung đỉnh.
Hình chóp tam giác đều S.ABCD có đáy ABCD là hình vuông nên\(CD = DA = BC = AB = 2a\)
Hình chóp tứ giác đều có các mặt bên là các tam giác cân bằng nhau có chung đỉnh nên \(SB = SC = SA = SD = a\) .
nên chọn đáp án A đúng
Cho hình chóp tứ giác đều có thể tích là \(50c{m^3}\), chiều cao hình chóp bằng \(5cm\). Tính diện tích mặt đáy của hình chóp đó.
-
A.
\(10c{m^2}\).
-
B.
\(30c{m^2}\)
-
C.
\(50c{m^2}\).
-
D.
\(\frac{{10}}{3}c{m^2}\).
Đáp án : B
Sử dụng công thức tính thể tích của hình chóp tứ giác đều: \(V = \frac{1}{3}.S.h\)
Theo công thức tính thể tích của hình chóp tứ giác đều: \(V = \frac{1}{3}.S.h\)
\( = > S = \frac{{3V}}{h} = \frac{{3.50}}{5} = 30c{m^2}\)
Cho hình chóp tứ giác đều S.ABCD có các mặt bên là các tam giác đều diện tích\(10c{m^2}\). Tính diện tích xung quanh của hình chóp đó.
-
A.
\(10c{m^2}\)
-
B.
\(20c{m^2}\)
-
C.
\(40c{m^2}\)
-
D.
\(30c{m^2}\).
Đáp án : C
Dựa vào đặc điểm của hình chóp tứ giác đều.
Hình chóp S.ABCD là hình chóp tứ giác đều, có 4 mặt bên, các mặt là các tam giác đều nên diện tích các mặt bằng nhau và cùng bằng \(10c{m^2}\). Vậy diện tích xung quanh của hình chóp S.ABCD là \(4.10 = 40c{m^2}\)
Cho hình chóp tứ giác đều có độ dài cạnh đáy là 3cm, độ dài trung đoạn bằng 5cm. Tính diện tích xung quanh hình chóp.
-
A.
\(10c{m^2}\)
-
B.
\(20c{m^2}\)
-
C.
\(40c{m^2}\)
-
D.
\(30c{m^2}\).
Đáp án : D
Dựa vào công thức tính diện tích xung quanh của hình chóp tứ giác đều:\({S_{xq}} = p.d\)
Nửa chu vi đáy của hình chóp: \(p = \frac{{3.4}}{2} = 6cm\)
Vậy diện tích xung quanh của hình chóp đã cho là \({S_{xq}} = p.d = 6.5 = 30c{m^2}\)
Cho hình chóp tứ giác đều có độ dài trung đoạn d, diện tích xung quanh là S. Chu vi đáy C bằng:
-
A.
\(C = {S_{xq}}.d\)
-
B.
\(C = \frac{{{S_{xq}}}}{{2d}}\)
-
C.
\(C = \frac{{{S_{xq}}}}{d}\)
-
D.
\(C = \frac{{2{S_{xq}}}}{d}\).
Đáp án : D
Dựa vào công thức diện tích xung quanh của hình chóp tứ giác đều: \({S_{xq}} = p.d\)
Gọi p là nửa chu vi đáy
\({S_{xq}} = p.d \Rightarrow p = \frac{{{S_{xq}}}}{d}\)
mà \(C = 2p \Rightarrow C = \frac{{2{S_{xq}}}}{d}\)
Cho khối chóp tứ giác đều, nếu tăng cạnh đáy lên ba lần và giảm chiều cao đi ba lần thì thể tích của khối chóp sẽ:
-
A.
Giảm đi 9 lần.
-
B.
Tăng lên 3 lần.
-
C.
Giảm đi 3 lần.
-
D.
Tăng lên 9 lần.
Đáp án : B
Dựa vào công thức tính thể tích khối chóp
Thể tích khối chóp tứ giác ban đầu là: \(V = \frac{1}{3}S.h = \frac{1}{3}a^2.h\)
\(S = a^2\) là diện tích đáy, h là chiều cao.
Nếu cạnh đáy tăng lên 3 lần thì diện tích đáy tăng 9 lần:
\(S_{mới} = (3a)^2 = 9a^2\).
Vì chiều cao giảm đi 3 lần nên \(h_{mới} = \frac{h}{3}\).
Khi đó, thể tích khối chóp mới là:
\(V_{mới} = \frac{1}{3}S_{mới}.h_{mới} = \frac{1}{3}. 9a^2.\frac{h}{3} = a^2h\)
Ta có: \(\frac{V_{mới}}{V} = \frac{a^2h}{\frac{1}{3}a^2.h} = 3\)
Vậy nếu cạnh đáy tăng lên 3 lần và chiều cao giảm đi 3 lần thì thể tích khối chóp tăng lên 3 lần.
Chọn phát biểu sai trong các phát biểu sau:
-
A.
Hình chóp tứ giác đều có các mặt bên là tam giác cân.
-
B.
Đường cao của hình chóp tứ giác đều là đoạn thẳng nối đỉnh của hình chóp và trung điểm một cạnh đáy.
-
C.
Đường cao kẻ từ đỉnh của mỗi mặt bên gọi là trung đoạn của hình chóp tứ giác đều.
-
D.
Diện tích xung quanh của hình chóp tứ giác đều bằng tích của nửa chu vi đáy với trung đoạn.
Đáp án : B
Dựa vào khái niệm hình chóp tứ giác đều, đường cao, trung đoạn, công thức tính diện tích xung quanh của hình chóp tứ giác đều.
Hình chóp tứ giác đều có đáy là hình vuông, các mặt bên là các tam giác cân bằng nhau có chung đỉnh nên câu A đúng,
Chân đường cao của hình chóp là điểm cách đều mỗi đỉnh của đáy nên câu B sai.
Đường cao kẻ từ đỉnh của mỗi mặt bên gọi là trung đoạn của hình chóp tứ giác đều nên câu C đúng.
Diện tích xung quanh của hình chóp tứ giác đều bằng tích của nửa chu vi đáy với trung đoạn nên câu D đúng.
Một hình chóp tứ giác đều có thể tích bằng \(32c{m^3}\), chiều cao hình chóp bằng 6cm, chiều cao mặt bên bằng 10cm. Tính diện tích xung quanh hình chóp đó.
-
A.
\(40(c{m^2})\)
-
B.
\(50(c{m^2})\)
-
C.
\(60(c{m^2})\)
-
D.
\(80(c{m^2})\)
Đáp án : D
B1: Tính diện tích đáy.
B2: Gọi x là độ dài cạnh đáy , tính diện tích đáy theo x, từ đó tìm được x.
B3: Tính diện tích một mặt bên.
B4: Tính diện tích xung quanh của hình chóp.
Diện tích đáy của hình chóp là : \(3.32:6 = 16c{m^2}\)
Gọi x là độ dài cạnh đáy, vì đáy hình chóp tứ giác đều là hình vuông nên ta có
\({x^2} = 16 \Rightarrow x = 4cm\).
Diện tích một mặt bên là: \(S = \frac{1}{2}.4.10 = 20(c{m^2})\)
Diện tích xung quanh của hình chóp trên là: \({S_{xq}} = 4.S = 4.20 = 80(c{m^2})\)
Cho hình chóp tứ giác đều S. ABCD có diện tích xung quanh bằng \(72c{m^2}\) , chiều cao có độ dài bằng 6cm, độ dài trung đoạn băng 4cm. Thể tích của khối chóp đó là?
-
A.
\(36c{m^3}\).
-
B.
\(162c{m^3}\).
-
C.
\(162\sqrt 3 c{m^3}\).
-
D.
\(72c{m^3}\).
Đáp án : B
B1: Tính độ dài cạnh đáy.
B2: Tính diện tích mặt đáy.
B3: Tính thể tích hình chóp đều theo công thức.
Gọi x là độ dài cạnh đáy, khi đó chu vi đáy bằng: 4x \( = > p = 2x\).
Diện tích xung quanh của hình chóp là: \({S_{xq}} = 72c{m^2}\)
\(\begin{array}{l} \Rightarrow p.d = 72\\ \Rightarrow 2x.4 = 72\\ \Rightarrow x = 9(cm)\end{array}\)
Độ dài cạnh đáy là: \(18.2:4 = 9cm\)
Diện tích mặt đáy là: \({S_{ABCD}} = 9.9 = 81c{m^2}\)
Áp dụng công thức thể tích khối chóp ta được: \(V = \frac{1}{3}.81.6 = 162c{m^3}\)
Tính diện tích toàn phần của hình chóp tứ giác đều biết cạnh đáy bằng 6cm, độ dài trung đoạn bằng 4cm.
-
A.
\(45c{m^2}\).
-
B.
\(81c{m^2}\).
-
C.
\(36c{m^2}\).
-
D.
\(84c{m^2}\).
Đáp án : D
B1: Tính nửa chu vi đáy
B2: Tính diện tích xung quanh của hình chóp đều: \({S_{xq}} = p.d\)
B3: Tính diện tích đáy
B4: Tính diện tích toàn phần của hình chóp tứ giác đều: \({S_{tp}} = {S_{xq}} + {S_{đáy}}\)
Nửa chu vi đáy của hình chóp: \(p = \frac{{6.4}}{2} = 12cm\)
Diện tích xung quanh của hình chóp là \({S_{xq}} = p.d = 12.4 = 48c{m^2}\)
Diện tích đáy của hình chóp là: \({S_{đáy}} = 6.6 = 36c{m^2}\)
Diện tích toàn phần của hình chóp tứ giác đều: \({S_{tp}} = {S_{xq}} + {S_{đáy}} = 48 + 36 = 84c{m^2}\)
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 4cm và chiều cao bằng 5cm. Tính độ dài trung đoạn của hình chóp đó.
-
A.
\(\frac{{\sqrt {17} }}{2}cm\).
-
B.
\(\sqrt {33} cm\).
-
C.
\(\sqrt {29} cm\).
-
D.
\(5cm\).
Đáp án : C
Sử dụng kiến thức về hình chóp đều, định lý Pythagore và độ dài trung đoạn để tính.
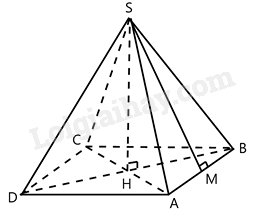
Gọi H là giao hai đường chéo của hình vuông ABCD , M là trung điểm AB.
Vì S.ABCD là hình chóp tứ giác đều nên các mặt bên là tam giác cân => tam giác SAB cân tại S => SM vừa là trung tuyến vừa là đường cao.
Xét tam giác vuông ABC có: \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{4^2} + {4^2}} = 4\sqrt 2 \Rightarrow AH = \frac{1}{2}.AC = 2\sqrt 2 cm\)
SH là chiều cao của hình chóp \( \Rightarrow SH = 5cm\)
Xét tam giác vuông SHA có: \(SA = \sqrt {S{H^2} + A{H^2}} = \sqrt {{5^2} + {{(2\sqrt 2 )}^2}} = \sqrt {33} cm\)
Xét tam giác vuông SAM có: \(SM = \sqrt {S{A^2} - A{M^2}} = \sqrt {{{(\sqrt {33} )}^2} - {{(2)}^2}} = \sqrt {29} cm\)
Cho hình chóp tứ giác đều S. ABCD có chu vi đáy là 20cm, chiều cao có số đo gấp 3 lần cạnh đáy. Thể tích của khối chóp đó là?
-
A.
\(80c{m^3}\).
-
B.
\(125c{m^3}\).
-
C.
\(25c{m^3}\).
-
D.
\(375c{m^3}\).
Đáp án : B
B1: Tính độ dài cạnh đáy và diện tích đáy.
B2: Tính chiều cao h của hình chóp tứ giác đều theo giả thiết
B3. Áp dụng công thức thể tích khối chóp \(V = \frac{1}{3}.S.h\)
Vì đáy hình chóp tứ giác đều S. ABCD là hình vuông, nên độ dài cạnh đáy là: \(20:4 = 5cm\)
Diện tích đáy hình chóp tứ giác đều là: \(S = 5.5 = 25c{m^2}\)
Chiều cao có số đo gấp 3 lần cạnh đáy nên h = 3.5=15cm
Áp dụng công thức thể tích khối chóp ta được: \(V = \frac{1}{3}.S.h = \frac{1}{3}.25.15 = 125c{m^3}\)
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau và bằng a. Thể tích V của khối chóp S.ABC.
-
A.
\(\frac{{{a^3}\sqrt 3 }}{2}\).
-
B.
\(\frac{{{a^3}\sqrt 3 }}{6}\).
-
C.
\(\frac{{{a^3}\sqrt 2 }}{6}\).
-
D.
\(\frac{{{a^3}}}{6}\).
Đáp án : C
Sử dụng kiến thức về hình chóp tứ giác đều, định lý Pythagore và diện tích tam giác đều để tính.
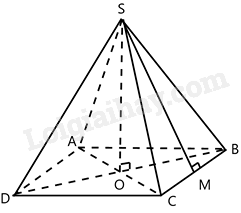
Gọi O là giao hai đường chéo của hình vuông ABCD , M là trung điểm BC.
Khi đó SO là chiều cao của hình chóp.
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\(AO = \frac{1}{2}.AC = \frac{1}{2}.a\sqrt 2 = \frac{{a\sqrt 2 }}{2}\)
\(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {{a^2} - {{(\frac{{a\sqrt 2 }}{2})}^2}} = \frac{{a\sqrt 2 }}{2}\)
Đáy ABCD là hình vuông nên diện tích đáy là: \({S_{ABCD}} = a.a = {a^2}\)
\({V_{ABCD}} = \frac{1}{3}.{S_{ABCD}}.SO = \frac{1}{3}.{a^2}.\frac{{a\sqrt 2 }}{2} = \frac{{{a^3}\sqrt 2 }}{6}\)
Cho mô hình dạng hình chóp tứ giác đều có diện tích bằng \(3600c{m^2}\), trung đoạn của khối gỗ là 80cm. Bạn Nam định sơn 4 mặt khối gỗ đó bằng sơn màu vàng, biết mỗi mét vuông bạn phải trả 50000 đồng tiền sơn. Hỏi bạn Nam sơn hết bao nhiêu tiền?
-
A.
48000 đồng.
-
B.
96000 đồng.
-
C.
24000 đồng.
-
D.
144000 đồng.
Đáp án : A
Sử dụng kiến thức về hình chóp tứ giác đều, chu vi, diện tích hình vuông và công thức tính diện tích xung quanh để tính.
B1: Tính độ dài cạnh đáy hình chóp.
B2: Tính nửa chu vi mặt đáy.
B3: Tính diện tích xung quanh của khối gỗ.
B4: Tính số tiền Nam cần phải trả.
Vì \(60.60 = 3600\) nên cạnh của mặt đáy bằng 60cm.
Chu vi mặt đáy là: \(C = 60.4 = 240(c{m^2}) \Rightarrow p = \frac{C}{2} = \frac{{240}}{2} = 120(c{m^2})\)
\({S_{xq}} = p.d = 120.80 = 9600c{m^2} = 0,96{m^2}\)
Bạn Nam sơn hết bao nhiêu tiền là: \(0,96.50000 = 48000\)(đồng)
Người ta làm một bugalow dạng hình chóp tứ giác đều có chiều cao 4m, cạnh sàn nhà bằng 6m. Người ta chia đôi làm hai tầng bằng một mặt phẳng song song với sàn, cách đỉnh của hình chóp một khoảng bằng nửa chiều cao, cạnh mặt sàn tầng hai bằng một nửa cạnh mặt sàn tầng một. Biết một người cần \(3{m^3}\)không khí, tính số người tối đa ở tầng dưới. ( hình vẽ dưới)

-
A.
16 người.
-
B.
20 người.
-
C.
18 người.
-
D.
14 người.
Đáp án : D
Sử dụng kiến thức về hình chóp tứ giác đều, thể tích hình chóp đều để tính.
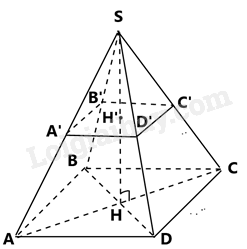
\(SH = 4m\)là chiều cao của bugalow
\( \Rightarrow SH' = \frac{{SH}}{2} = 2m\)
\(A'B' = \frac{1}{2}.AB = \frac{1}{2}.6 = 3m\)
Ta có:
\(\begin{array}{l}{S_{A'B'C'D'}} = 3.3 = 9{m^2}\\{S_{ABCD}} = 6.6 = 36{m^2}\end{array}\)
\(\begin{array}{l}{V_{S.A'B'C'D'}} = \frac{1}{3}.{S_{A'B'C'D'}}.SH' = \frac{1}{3}.9.2 = 6{m^3}\\{V_{S.ABCD}} = \frac{1}{3}.{S_{ABCD}}.SH = \frac{1}{3}.36.4 = 48{m^3}\end{array}\)
Thể tích phần không gian còn lại ở tầng dưới là: \(V = {V_{S.ABCD}} - {V_{S.A'B'C'D'}} = 48 - 6 = 42{m^3}\)
Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng a, cạnh bên bằng 2a. Gọi I, H lần lượt là trung điểm cạnh AB, CD. Tính thể tích V của khối chóp S.IBCH.
-
A.
\(V = \frac{{{a^3}\sqrt 2 }}{{12}}\).
-
B.
\(V = \frac{{{a^3}\sqrt 2 }}{6}\).
-
C.
\(V = \frac{{{a^3}\sqrt 2 }}{4}\).
-
D.
\(V = \frac{{{a^3}\sqrt 2 }}{8}\).
Đáp án : A
Sử dụng kiến thức về hình chóp đều, định lý Pythagore và diện tích tam giác đều để tính.
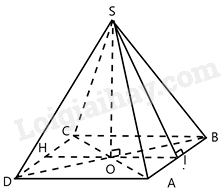
Tứ giác ABCD là hình vuông cạnh a nên diện tích ABCD bằng: \({S_{ABCD}} = {a^2}\)
Xét tam giác vuông ABC có: \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \Rightarrow AO = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác vuông SOA có: \(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {{a^2} - {{(\frac{{a\sqrt 2 }}{2})}^2}} = \frac{{a\sqrt 2 }}{2}\)
\({V_{SABCD}} = \frac{1}{3}.{S_{ABCD}}.SO = \frac{1}{3}.{a^2}.\frac{{a\sqrt 2 }}{2} = \frac{1}{3}.{a^2}.\frac{{a\sqrt 2 }}{2} = \frac{{{a^3}\sqrt 2 }}{6}\)
\(\frac{{{V_{SIBCH}}}}{{{V_{SABCD}}}} = \frac{{\frac{1}{3}.{S_{IBCH}}.h}}{{\frac{1}{3}.{S_{ABCD}}.h}} = \frac{{{S_{IBCH}}}}{{{S_{ABCD}}}} = \frac{{IB.BC}}{{AB.BC}} = \frac{{BI}}{{AB}} = \frac{1}{2} = > {V_{SIBCH}} = \frac{1}{2}{V_{SABCD}} = \frac{1}{2}.\frac{{{a^3}\sqrt 2 }}{6} = \frac{{{a^3}\sqrt 2 }}{{12}}\)